文章目录

写在前面
正交基与投影
高维投影和Gram-Schmidt过程
- 三维空间
- 四维及以上空间
Gram-Schmidt过程构造标准正交基
后记
- Section 4.1中的应用
- Section 5.2中的应用
题外话
- 两个定理
- 微分方程求解

写在前面

原论文标题：Distributed convex optimization via continuous-time coordination algorithms with discrete-time communication.

之所以想要写这篇文章，是因为最近在看的一篇分布式优化论文(Kia 2015)¹，其中有这么一个问题。

令Πn=In−1n1n1nT\Pi_n=I_n-\frac{1}{n}1_n 1_n^TΠn=In−n11n1nT。为了简便表示，可以定义r∈Rnr\in\mathbb R^nr∈Rn和R∈Rn×(n−1)R\in\mathbb R^{n\times (n-1)}R∈Rn×(n−1)，且满足以下条件：
r=1n1n，rTR=0，RTR=In−1，RRT=Πn。r=\frac{1}{\sqrt{n}} 1_n，\,r^TR= 0，\,R^TR=I_{n-1}，\,RR^T=\Pi_n。 r=n11n，rTR=0，RTR=In−1，RRT=Πn。
那么如何得到期望的RRR？

显然这里，[r,R][r, R][r,R]是nnn维空间的一组标准正交基(orthonormal basis)。现在已知rrr需要求出所有RRR的列向量。这就需要线性代数中标准正交基和投影的知识。

正交基与投影

一个nnn维空间中任何一组线性无关(linearly independent)的向量，都是这个nnn维空间的一组基。当这组基的向量两两垂直(即eiTej=0e_i^Te_j=0eiTej=0)，则称为正交基(orthogonal basis)。而标准正交基只是将正交基又添加了一个条件，模长为1(即∥ei∥=1\|e_i\|=1∥ei∥=1)。一个空间可以有无数组基向量，正交基和标准正交基也同样是有无数组的。

一维投影相当于把一个向量投影到另一个向量，可以进一步求取正交基。以下图片来自Jakob_Hu的博客²。

已知向量uuu和vvv，按照如上图所示方法可以求取投影p=uTv∥u∥2up=\frac{u^Tv}{\|u\|^2}up=∥u∥2uTvu。求出ppp后，进一步求出正交向量v−pv-pv−p非常容易。这就解决了在二维空间中求取一组正交基的问题，正交基为ppp和v−pv-pv−p。

高维投影和Gram-Schmidt过程

为了解决第一节提到的问题，我们需要一个能够通过任意维度的一组基构造空间的正交基的算法。

三维空间

以三维向量为例，假设存在一组三维向量，需要求出这三个向量所在空间的正交基，其中两个已经处理得到相互正交的向量p1p_1p1、p2p_2p2。再加上向量www构成三维空间的一组基。

下一步我们需要做www向p1p_1p1、p2p_2p2构成的二维子空间的投影ppp，则w−pw-pw−p即我们想要的正交向量。

分别做www向p1p_1p1、p2p_2p2上的投影，得到wTp1∥p1∥2p1\frac{w^Tp_1}{\|p_1\|^2}p_1∥p1∥2wTp1p1和wTp2∥p2∥2p2\frac{w^Tp_2}{\|p_2\|^2}p_2∥p2∥2wTp2p2，则p=wTp1∥p1∥2p1+wTp2∥p2∥2p2p=\frac{w^Tp_1}{\|p_1\|^2}p_1+\frac{w^Tp_2}{\|p_2\|^2}p_2p=∥p1∥2wTp1p1+∥p2∥2wTp2p2；
计算w−pw-pw−p，得到w−wTp1∥p1∥2p1−wTp2∥p2∥2p2w-\frac{w^Tp_1}{\|p_1\|^2}p_1-\frac{w^Tp_2}{\|p_2\|^2}p_2w−∥p1∥2wTp1p1−∥p2∥2wTp2p2即第三维的正交向量。

三维空间求正交基的整个过程可以看做是先求出相应的二维空间的正交基，进一步求取三维空间正交基。

四维及以上空间

与三维空间相似，先求取低维度空间的正交基，在其基础上进行高一维度正交基的求取。

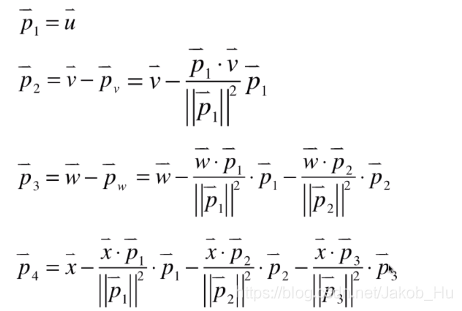
给出任何一组nnn维空间的基，正交基的过程都可以通过逐一维度的计算得到。任何一个维度的向量都减去它在低维度空间中已经正交的向量的投影，这一过程就是Gram-Schmidt过程。

Gram-Schmidt过程构造标准正交基

回到第一节提到的问题，现在我们已知nnn维空间的任意一个向量rrr，如何利用Gram-Schmidt过程构造一组标准正交基。

% 维度为4
n = 4;
r = ones(n,1)/n;% r'的零空间
N = @(A) eye(size(A,2))-pinv(A)*A;
R1 = N(r');
R1 = R1./vecnorm(R1);% [r R1(:,1)]'的零空间
R2 = N([r R1(:,1)]');
R2 = R2./vecnorm(R2);% [r R1(:,1) R2(:,2)]'的零空间
R3 = N([r R1(:,1) R2(:,2)]');
R3 = R3./vecnorm(R3);
R = [R1(:,1) R2(:,2) R3(:,3)];

由此构建第一节需要的RRR。

后记

这里最后提一下，按照前面这样定义的RRR会有什么好的性质。

首先，自不必说，有，
r=1n1n，rTR=0，RTR=In−1，RRT=Πn。r=\frac{1}{\sqrt{n}}\boldsymbol 1_n，\,r^TR=\boldsymbol 0，\,R^TR=I_{n-1}，\,RR^T=\Pi_n。 r=n11n，rTR=0，RTR=In−1，RRT=Πn。
然后，P=[r,R]P=[r,R]P=[r,R]显然是标准正交基组成的矩阵。由于PPP满秩，所以
PTP=PPT=In，RTP=[0n−1,In−1]，ΠnP=RRTP=R[0n−1,In−1]=[0n−1,R]。P^TP=PP^T=I_n，\,R^TP=[0_{n-1},I_{n-1}]，\, \Pi_n P=RR^TP=R[0_{n-1},I_{n-1}]=[0_{n-1},R]。 PTP=PPT=In，RTP=[0n−1,In−1]，ΠnP=RRTP=R[0n−1,In−1]=[0n−1,R]。
下面给出该性质在第一节所看论文中的应用。

Section 4.1中的应用

定义图G\mathcal GG是强连通平衡图，其拉普拉斯矩阵为LLL。现有动力学如下
v˙=αβLx，x˙=−α∇f(x)−βLx−v，\begin{aligned} \dot v&=\alpha\beta Lx，\\ \dot x&=-\alpha\nabla f(x)-\beta Lx-v， \end{aligned} v˙x˙=αβLx，=−α∇f(x)−βLx−v，
其中1nTv=01_n^Tv=01nTv=0，故也有rTv=0r^Tv=0rTv=0。令vˉ=−α∇f(xˉ)\bar v=-\alpha\nabla f(\bar x)vˉ=−α∇f(xˉ)。

定义坐标变换
u=v−vˉ，y=x−xˉ，u=Pw，y=Pz。\begin{aligned} u&=v-\bar v，\,&y &=x-\bar x，\\ u&=Pw，\,&y&=Pz。 \end{aligned} uu=v−vˉ，=Pw，yy=x−xˉ，=Pz。
由于拉普拉斯矩阵的性质，PTLP=diag⁡(0,RTLR)P^TLP=\operatorname{diag}( 0,R^TLR)PTLP=diag(0,RTLR)。同时，rTPw=rT(v−vˉ)=rTvˉr^TPw=r^T(v-\bar v)=r^T\bar vrTPw=rT(v−vˉ)=rTvˉ，RTPw=w2:nR^TPw=w_{2:n}RTPw=w2:n。

定义h=∇f(y+xˉ)−∇f(xˉ)h=\nabla f(y+\bar x)-\nabla f(\bar x)h=∇f(y+xˉ)−∇f(xˉ)，有
w˙1=0，w˙2:n=αβRTLRz2:n，z˙1=−αrTh，z˙2:n=−αRTh−βRTLRz2:n−w2:n。\begin{aligned} \dot w_1&=0，\\ \dot w_{2:n}&=\alpha\beta R^TLRz_{2:n}，\\ \dot z_1&=-\alpha r^Th，\\ \dot z_{2:n}&=-\alpha R^Th-\beta R^TLRz_{2:n}-w_{2:n}。 \end{aligned} w˙1w˙2:nz˙1z˙2:n=0，=αβRTLRz2:n，=−αrTh，=−αRTh−βRTLRz2:n−w2:n。

Section 5.2中的应用

令z~2:n(t)=z2:n(tk)−z2:n(t)=RTP(z(tk)−z(t))=RT(x(tk)−x(t))\tilde z_{2:n}(t)=z_{2:n}(t_k)-z_{2:n}(t)=R^TP(z(t_k)-z(t))=R^T(x(t_k)-x(t))z~2:n(t)=z2:n(tk)−z2:n(t)=RTP(z(tk)−z(t))=RT(x(tk)−x(t))，则有
z~2:nT(t)z~2:n(t)=(x(tk)−x(t))TRRT(x(tk)−x(t))=(x(tk)−x(t))TΠ(x(tk)−x(t))。\tilde z_{2:n}^T(t)\tilde z_{2:n}(t)=(x(t_k)-x(t))^TRR^T(x(t_k)-x(t))=(x(t_k)-x(t))^T\Pi(x(t_k)-x(t))。 z~2:nT(t)z~2:n(t)=(x(tk)−x(t))TRRT(x(tk)−x(t))=(x(tk)−x(t))TΠ(x(tk)−x(t))。
由于Π\PiΠ是幂等的，即Π=Π2\Pi=\Pi^2Π=Π2。因此，∥z~2:n(t)∥=∥Π(x(tk)−x(t))∥\|\tilde z_{2:n}(t)\|=\|\Pi(x(t_k)-x(t))\|∥z~2:n(t)∥=∥Π(x(tk)−x(t))∥。

令p=[zT,w2:nT]Tp=[z^T,w_{2:n}^T]^Tp=[zT,w2:nT]T，同样的由于Π\PiΠ的幂等性，有
pTp=zTz+w2:nTw2:n=yTPPTy+wPTRRTPw=(x−xˉ)T(x−xˉ)+(v−vˉ)TΠ(v−vˉ)p^Tp=z^Tz+w_{2:n}^Tw_{2:n}=y^TPP^Ty+wP^TRR^T Pw=(x-\bar x)^T(x-\bar x)+(v-\bar v)^T\Pi(v-\bar v) pTp=zTz+w2:nTw2:n=yTPPTy+wPTRRTPw=(x−xˉ)T(x−xˉ)+(v−vˉ)TΠ(v−vˉ)
因此，∥p∥=∥x−xˉ∥2+∥Π(v−vˉ)∥2\|p\|=\sqrt{\|x-\bar x\|^2+\|\Pi(v-\bar v)\|^2}∥p∥=∥x−xˉ∥2+∥Π(v−vˉ)∥2。

题外话

此外，简单记录下第一节所看论文的另外一些收获。

两个定理

证明收敛性和有界性用到的两个定理³。

Lemma 3.4. (Comparison lemma) Consider the scalar differential equation
u˙=f(t,u),u(t0)=u0\dot u=f(t,u),\,u(t_0)=u_0 u˙=f(t,u),u(t0)=u0
where f(t,u)f(t,u)f(t,u) is continuous in ttt and locally Lipschitz in uuu, for all t≥0t\geq 0t≥0 and all u∈J⊂Ru\in J\subset \mathbb Ru∈J⊂R. Let [t0,T)[t_0,T)[t0,T) (TTT could be infinity) be the maximal interval of existence of the solution u(t)u(t)u(t) and suppose u(t)∈Ju(t)\in Ju(t)∈J for all t∈[t0,T)t\in[t_0,T)t∈[t0,T). Let v(t)v(t)v(t) be a continuous function whose upper right-hand derivative D+v(t)D^+v(t)D+v(t) satisfies the differential inequality
D+v(t)≤f(t,v(t)),v(t0)≤u0,D^+v(t)\leq f(t,v(t)),\,v(t_0)\leq u_0, D+v(t)≤f(t,v(t)),v(t0)≤u0,
with v(t)∈Jv(t)\in Jv(t)∈J for all t∈[t0,T)t\in[t_0,T)t∈[t0,T). Then, v(t)≤u(t)v(t)\leq u(t)v(t)≤u(t) for all t∈[t0,T)t\in[t_0,T)t∈[t0,T).

可以知道，当v˙(t)≤u˙(t)\dot v(t)\leq \dot u(t)v˙(t)≤u˙(t)且v(t0)≤u(t0)v(t_0)\leq u(t_0)v(t0)≤u(t0)时，v(t)≤u(t)v(t)\leq u(t)v(t)≤u(t)。

Theorem 4.10. Let x=0x=0x=0 be an equilibrium point for x˙=f(t,x)\dot x=f(t,x)x˙=f(t,x) and D⊂RnD\subset \mathbb R^nD⊂Rn be a domain containing x=0x=0x=0. Let V:[0,∞)×D→RV:[0,\infty)\times D\to \mathbb RV:[0,∞)×D→R be a continuously differentiable function such that
k1∥x∥α≤V(t,x)≤k2∥x∥α,∂V∂t+∂V∂xf(t,x)≤−k3∥x∥α,\begin{aligned} k_1\|x\|^\alpha\leq V(t,x)&\leq k_2\|x\|^\alpha,\\ \frac{\partial V}{\partial t}+\frac{\partial V}{\partial x}f(t,x)&\leq -k_3\|x\|^\alpha, \end{aligned} k1∥x∥α≤V(t,x)∂t∂V+∂x∂Vf(t,x)≤k2∥x∥α,≤−k3∥x∥α,
∀t≥0\forall t\geq 0∀t≥0 and ∀x∈D\forall x\in D∀x∈D, where k1k_1k1, k2k_2k2, k3k_3k3, and aaa are positive constants. Then, x=0x=0x=0 is exponentially stable. If the assumptions hold globally, then x=0x=0x=0 is globally exponentially stable.

可以知道，当上述定理中的条件满足时，我们有V˙≤−k3k2V\dot V\leq -\frac{k_3}{k_2}VV˙≤−k2k3V，即不光指数收敛，且收敛速度不小于k3k2\frac{k_3}{k_2}k2k3。

由Lemma 3.4可知，
V(t,x(t))≤V(t0,x(t0))e−(k3/k2)(t−t0)。V(t,x(t))\leq V(t_0,x(t_0))e^{-(k_3/k_2)(t-t_0)}。 V(t,x(t))≤V(t0,x(t0))e−(k3/k2)(t−t0)。
因此，
∥x(t)∥≤[V(t,x(t))k1]1/α≤[V(t0,x(t0))e−(k3/k2)(t−t0)k1]1/α≤[k2∥x(t0)∥αe−(k3/k2)(t−t0)k1]1/α=(k2k1)1/α∥x(t0)∥e−(k3/k2a)(t−t0)。\begin{aligned} \|x(t)\|&\leq \left[\frac{V(t,x(t))}{k_1}\right]^{1/\alpha}\leq\left[\frac{V(t_0,x(t_0))e^{-(k_3/k_2)(t-t_0)}}{k_1}\right]^{1/\alpha}\\ &\leq \left[\frac{k_2\|x(t_0)\|^\alpha e^{-(k_3/k_2)(t-t_0)}}{k_1}\right]^{1/\alpha}=\left(\frac{k_2}{k_1}\right)^{1/\alpha}\|x(t_0)\|e^{-(k_3/k_2a)(t-t_0)}。 \end{aligned} ∥x(t)∥≤[k1V(t,x(t))]1/α≤[k1V(t0,x(t0))e−(k3/k2)(t−t0)]1/α≤[k1k2∥x(t0)∥αe−(k3/k2)(t−t0)]1/α=(k1k2)1/α∥x(t0)∥e−(k3/k2a)(t−t0)。

微分方程求解

使用Lemma 3.4证明收敛性，本质是把一个复杂的微分方程求解问题，转化成一个相对容易的微分方程来求解。

以第一节所看论文中证明有界性时的一个问题为例。已知
x˙≤a(1+x)+b(1+x)2,x(0)=0\dot x\leq a(1+x)+b(1+x)^2,\,x(0)=0 x˙≤a(1+x)+b(1+x)2,x(0)=0
现在要证明xxx在时间τ\tauτ内有界ζ\zetaζ，并求出τ\tauτ的值。

应用Lemma 3.4，若存在y˙=a(1+y)+b(1+y)2\dot y=a(1+y)+b(1+y)^2y˙=a(1+y)+b(1+y)2，y(0)=0y(0)=0y(0)=0，那么x≤yx\leq yx≤y，∀t≥0\forall t\geq 0∀t≥0。

分离变量，求解微分方程，参考步骤⁴如下
t+C=∫dt=∫dya(1+y)+b(1+y)2=∫dyb(1+y+a2b)2−a24b=1b∫dzz2−a24b2,(z=1+y+a2b)=1a∫(dzz−a2b−dzz+a2b)=1aln⁡∣z−a2b∣−1aln⁡∣z+a2b∣=1aln⁡∣1+y∣−1aln⁡∣1+y+ab∣\begin{aligned} t+C=\int dt &=\int \frac{dy}{a(1+y)+b(1+y)^2}\\ &=\int \frac{dy}{b\left(1+y+\frac{a}{2b}\right)^2-\frac{a^2}{4b}}\\ &=\frac{1}{b}\int \frac{dz}{z^2-\frac{a^2}{4b^2}} ,\quad \left(z=1+y+\frac{a}{2b}\right)\\ &=\frac{1}{a}\int \left(\frac{dz}{z-\frac{a}{2b}}-\frac{dz}{z+\frac{a}{2b}}\right)\\ &=\frac{1}{a}\ln \left|z-\frac{a}{2b}\right|-\frac{1}{a}\ln \left|z+\frac{a}{2b}\right|\\ &=\frac{1}{a}\ln \left|1+y\right|-\frac{1}{a}\ln \left|1+y+\frac{a}{b}\right| \end{aligned} t+C=∫dt=∫a(1+y)+b(1+y)2dy=∫b(1+y+2ba)2−4ba2dy=b1∫z2−4b2a2dz,(z=1+y+2ba)=a1∫(z−2badz−z+2badz)=a1ln∣∣∣z−2ba∣∣∣−a1ln∣∣∣z+2ba∣∣∣=a1ln∣1+y∣−a1ln∣∣∣1+y+ba∣∣∣
假设y,a,b≥0y,a,b\geq 0y,a,b≥0。令y=t=0y=t=0y=t=0，可得aC=ln⁡(ba+b)aC=\ln (\frac{b}{a+b})aC=ln(a+bb)，则有
eat+aC=ba+beat=by+bby+a+be^{at+aC}=\frac{b}{a+b}e^{at}=\frac{by+b}{by+a+b} eat+aC=a+bbeat=by+a+bby+b
变换为yyy关于ttt的函数
y(t,0)=(a+b)(eat−1)−beat+a+by(t,0)=\frac{(a+b)(e^{at}-1)}{-be^{at}+a+b} y(t,0)=−beat+a+b(a+b)(eat−1)
再令y(τ,0)=ζy(\tau,0)=\zetay(τ,0)=ζ，得到
τ=1aln⁡(1+aζa+b(1+ζ))\tau=\frac{1}{a}\ln\left(1+\frac{a\zeta}{a+b(1+\zeta)}\right) τ=a1ln(1+a+b(1+ζ)aζ)

Kia, S. S., Cortés, J., & Martínez, S. (2015). Distributed convex optimization via continuous-time coordination algorithms with discrete-time communication. In Automatica (Vol. 55, pp. 254–264). Elsevier Ltd. https://doi.org/10.1016/j.automatica.2015.03.001 ↩︎
Jakob_Hu. 线性代数(14)——正交性、标准正交基和投影. https://blog.csdn.net/Jakob_Hu/article/details/90813435 ↩︎
Khalil, H. K. (2002). Nonlinear systems (3rd ed.). Prentice Hall, ISBN: 0130673897. ↩︎
积分(反导数)计算器. https://zs.symbolab.com/solver/integral-calculator ↩︎

【论文笔记】标准正交基和投影在分布式控制中的应用相关推荐

论文笔记——HDD算法：异构网络中信息扩散的深度学习方法
HDD算法发表在knowledge-Based Systems上的一篇文章.有许多现实世界的复杂系统与多类型相互作用的实体,可以被视为异构网络,包括人类连接和生物进化.这类网络的主要问题之一是预测信 ...
【论文笔记：场景】边缘计算中分布式协作的动态卸载模型:森林火灾管理的一个用例
[摘要]:随着物联网(IoT)的发展,数据量不断增长并变得更加多样化.将数据传输到云端时存在几个问题,例如网络带宽和延迟的限制.这引起了人们对边缘计算研究的极大兴趣,边缘计算处理和分析数据导致的网络终 ...
【论文-笔记】海防雷达仿真系统中PPI的设计与实现
摘要重点介绍: 仿真系统中的PPI. 提出了矩阵融合法,实现雷达余晖效果,通过衰减矩阵来控制位图中任一维颜色向量,相对于逐点消隐法的速度提升较大. 针对干扰模型进行研究,构造出适用于雷达的干扰模型. ...
经验 | 深度学习中从基础综述、论文笔记到工程经验、训练技巧
点上方蓝字计算机视觉联盟获取更多干货在右上方 ··· 设为星标 ★,与你不见不散仅作学术分享,不代表本公众号立场,侵权联系删除转载于:本文授权转自知乎作者跑者小越,https://zhuanla ...
论文笔记 -- Communication Lower Bound in Convolution Accelerators 卷积加速器中的通信下界
论文笔记 – Communication Lower Bound in Convolution Accelerators 卷积加速器中的通信下界 @(论文笔记) 文章目录论文笔记 -- Commun ...
《使用机器视觉从照片中确定西瓜质量》论文笔记
<使用机器视觉从照片中确定西瓜质量>论文笔记链接:Watermelon Quality Determining from a Photo Using Machine Vision | I ...
【模糊综合评价的运用】——《电子舌技术在食用盐模糊感官评价中的应用》论文笔记（内附MATLAB程序）
[模糊综合评价的运用]--<电子舌技术在食用盐模糊感官评价中的应用>论文笔记(内附MATLAB程序) 本文目录 1.因素集:(评价指标集)与评价事物相关的因素. 2. 评语集:(评价的结果 ...
【论文阅读笔记】从在线开发者聊天中自动提取基于意见的问答
论文标题:Automatic Extraction of Opinion-based Q&A from Online Developer Chats 原文链接:https://ieeexplo ...
「ArXiv2020」【Efficient Transformers: A Survey】论文笔记（更新中）
「ArXiv2020」[Efficient Transformers: A Survey]论文笔记 Abstract 1. Introduction 2. Background on Transfor ...

【论文笔记】标准正交基和投影在分布式控制中的应用