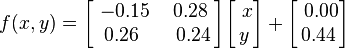http://www.matrix67.com/blog/archives/500

矩阵、随机化与分形图形

Stetson大学的一个非常可爱的MM（以后本Blog将简称她为Stetson MM）和我分享了一个很神奇的东西。她们正在做一个线性代数的课题研究，题目的大致意思是“用矩阵来构造分形图形”。Stetson MM叫我试着做下面这个实验：对于一个坐标点(x,y)，定义下面4个矩阵变换：

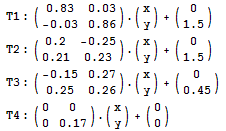
然后，初始时令(x,y)等于(0,0)，按照 T1 – 85%, T2 – 6%, T3 – 8%, T4 – 1% 的概率，随机选择一个变换对该点进行操作，生成的点就是新的(x,y)；把它画在图上后，再重复刚才的操作，并一直这样做下去。

ClearAll["Global`*"];
list = {{0, 0}};
last = {{0}, {0}};
For[i = 0, i < 50000, i++, r = Random[];If[r < 0.85, last = {{0.83, 0.03}, {-0.03, 0.86}}.last + {{0}, {1.5}}, If[r < 0.91, last = {{0.2, -0.25}, {0.21, 0.23}}.last + {{0}, {1.5}}, If[r < 0.99, last = {{-0.15, 0.27}, {0.25, 0.26}}.last + {{0}, {0.45}}, last = {{0, 0}, {0, 0.17}}.last + {{0}, {0}}]]];list = Append[list, First[Transpose[last]]];]
h = ListPlot[list, PlotStyle -> {PointSize[0.002], Red}, Axes -> False];
range = First /@ Differences /@ (PlotRange /. Options[h]);
Show[h, AspectRatio -> Last@range/First@range]

或者:

ClearAll["Global`*"];
list = {{0, 0}};
last = {{0}, {0}};
GetNextPoint[pt_] := Module[{r,t1 = {{0.83, 0.03}, {-0.03, 0.86}}, p1 = {0, 1.5},t2 = {{0.2, -0.25}, {0.21, 0.23}}, p2 = {0, 1.5},t3 = {{-0.15, 0.27}, {0.25, 0.26}}, p3 = {0, 0.45},t4 = {{0, 0}, {0, 0.17}}, p4 = {0, 0}},r = Random[];If[r <= 0.85, t1.pt + p1, If[r <= 0.91, t2.pt + p2, If[r <= 0.99, t3.pt + p3, t4.pt + p4]]]]
For[i = 0, i < 50000, i++, last = GetNextPoint[last];list = Append[list, First[Transpose[last]]];]
h = ListPlot[list, PlotStyle -> {PointSize[0.005], Red}, Axes -> False];
range = First /@ Differences /@ (PlotRange /. Options[h]);
Show[h, AspectRatio -> Last@range/First@range]

ClearAll["Global`*"];
t0 = AbsoluteTime[];
list = {{0, 0}};
last = {{0}, {0}};
GetNextPoint[pt_] := Module[{r, t1 = Transpose[Reverse[Transpose[Reverse[{{0.83, 0.03}, {-0.03, 0.86}}]]]], p1 = Reverse[{0, 1.5}], t2 = Transpose[Reverse[Transpose[Reverse[{{0.2, -0.25}, {0.21, 0.23}}]]]], p2 = Reverse[{0, 1.5}], t3 = Transpose[Reverse[Transpose[Reverse[{{-0.15, 0.27}, {0.25, 0.26}}]]]], p3 = Reverse[{0, 0.45}], t4 = Transpose[Reverse[Transpose[Reverse[{{0, 0}, {0, 0.17}}]]]], p4 = Reverse[{0, 0}]}, r = Random[];If[r <= 0.85, t1.pt + p1, If[r <= 0.91, t2.pt + p2, If[r <= 0.99, t3.pt + p3, t4.pt + p4]]]]
For[i = 0, i < 100000, i++, last = GetNextPoint[last];list = Append[list, First[Transpose[last]]];]
h = ListPlot[list, PlotStyle -> {PointSize[0.002], Green}, Axes -> False, Background -> Black];
range = First /@ Differences /@ (PlotRange /. Options[h]);
Show[h, AspectRatio -> Last@range/First@range]
Print[AbsoluteTime[] - t0]

用下面的代码可以提速数十倍:

Clear["`*"];
t0 = AbsoluteTime[];
ifs[prob_, A_, init_, maxIter_] := FoldList[#2.{#[[1]], #[[2]], 1} &, init, RandomChoice[prob -> A, maxIter]];init = {0., 0.};
prob = N@{85, 6, 8, 1};
A = N@{{{0.83, 0.03, 0}, {-0.03, 0.86, 1.5}}, {{0.2, -0.25, 0}, {0.21,0.23, 1.5}}, {{-0.15, 0.27, 0}, {0.25, 0.26, 0.45}}, {{0, 0, 0}, {0, 0.17, 0}}};
iter = 10^5;
pts = ifs[prob, A, init, iter];
Graphics[{PointSize[0.002], Green, Point[pts]}, Background -> Black]
(*h=ListPlot[pts,PlotStyle\[Rule]Green,Background\[Rule]Black];
range=First/@Differences/@(PlotRange/.Options[h]);Show[h,AspectRatio\
\[Rule]Last@range/First@range,Axes->False]*)
Print[AbsoluteTime[] - t0]

这类经典问题,维基上总是有答案的:

http://en.wikipedia.org/wiki/Barnsley_fern

The Barnsley Fern is a fractal named after the British mathematician Michael Barnsley who first described it in his bookFractals Everywhere.^[1] He made it to resemble the Black Spleenwort, Asplenium adiantum-nigrum.

[hide]

1 History
2 Construction
- 2.1 Computer generation
- 2.2 Mutant varieties
3 References

History[edit]

The fern is one of the basic examples of self-similar sets, i.e. it is a mathematically generated pattern that can be reproducible at any magnification or reduction. Like the Sierpinski triangle, the Barnsley fern shows how graphically beautiful structures can be built from repetitive uses of mathematical formulas with computers. Barnsley's book about fractals is based on the course which he taught for undergraduate and graduate students in the School of Mathematics, Georgia Institute of Technology, called Fractal Geometry. After publishing the book, a second course was developed, called Fractal Measure Theory.^[1] Barnsley's work has been a source of inspiration to graphic artists attempting to imitate nature with mathematical models.

The fern code developed by Barnsley is an example of an iterated function system (IFS) to create a fractal. He has used fractals to model a diverse range of phenomena in science and technology, but most specifically plant structures.

"IFSs provide models for certain plants, leaves, and ferns, by virtue of the self-similarity which often occurs in branching structures in nature. But nature also exhibits randomness and variation from one level to the next; no two ferns are exactly alike, and the branching fronds become leaves at a smaller scale. V-variable fractals allow for such randomness and variability across scales, while at the same time admitting a continuous dependence on parameters which facilitates geometrical modelling. These factors allow us to make the hybrid biological models...

...we speculate that when a V -variable geometrical fractal model is found that has a good match to the geometry of a given plant, then there is a specific relationship between these code trees and the information stored in the genes of the plant.

—Michael Barnsley et al.^[2]

Construction[edit]

Real lady ferns.

Barnsley's fern uses four affine transformations. The formula for one transformation is the following:

Barnsley shows the IFS code for his Black Spleenwort fern fractal as a matrix of values shown in a table.^[1] In the table, the columns "a" through "f" are the coefficients of the equation, and "p" represents the probability factor.

w	a	b	c	d	f	p
ƒ₁	0	0	0	0.16	0	0.01
ƒ₂	0.85	0.04	−0.04	0.85	1.6	0.85
ƒ₃	0.2	−0.26	0.23	0.22	1.6	0.07
ƒ₄	−0.15	0.28	0.26	0.24	0.44	0.07

These correspond to the following transformations:

Computer generation[edit]

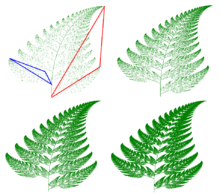
Fractal fern in four states of construction. Highlighted triangles show how the half of one leaflet is transformed to half of one wholeleaf or frond.

Though Barnsley's fern could in theory be plotted by hand with a pen and graph paper, the number of iterations necessary runs into the tens of thousands, which makes use of a computer practically mandatory. Many different computer models of Barnsley's fern are popular with contemporary mathematicians. As long as the math is programmed correctly using Barnsley's matrix of constants, the same fern shape will be produced.

The first point drawn is at the origin (x₀ = 0, y₀ = 0) and then the new points are iteratively computed by randomly applying one of the following four coordinate transformations:^[3]^[4]

ƒ₁

x_{n + 1} = 0

y_{n + 1} = 0.16 y_n.

This coordinate transformation is chosen 1% of the time and just maps any point to a point in the first line segment at the base of the stem. This part of the figure is the first to be completed in during the course of iterations.

ƒ₂

x_{n + 1} = 0.85 x_n + 0.04 y_n

y_{n + 1} = −0.04 x_n + 0.85 y_n + 1.6.

This coordinate transformation is chosen 85% of the time and maps any point inside the leaflet represented by the red triangle to a point inside the opposite, smaller leaflet represented by the blue triangle in the figure.

ƒ₃

x_{n + 1} = 0.2 x_n − 0.26 y_n

y_{n + 1} = 0.23 x_n + 0.22 y_n + 1.6.

This coordinate transformation is chosen 7% of the time and maps any point inside the leaflet (or pinna) represented by the blue triangle to a point inside the alternating corresponding triangle across the stem (it flips it).

ƒ₄

x_{n + 1} = −0.15 x_n + 0.28 y_n

y_{n + 1} = 0.26 x_n + 0.24 y_n + 0.44.

The first coordinate transformation draws the stem. The second generates successive copies of the stem and bottom fronds to make the complete fern. The third draws the bottom frond on the left. The fourth draws the bottom frond on the right. The recursive nature of the IFS guarantees that the whole is a larger replica of each frond. Note that the complete fern is within the range −2.1820 < x < 2.6558 and 0 ≤ y < 9.9983.

Mutant varieties[edit]

Barnsley fern mutated into aThelypteridaceae fern.

Barnsley fern mutated into aleptosporangiate fern.

By playing with the coefficients, it is possible to create mutant fern varieties. In his paper on V-variable fractals, Barnsley calls this trait a superfractal.^[2]

One experimenter has come up with a table of coefficients to produce another remarkably naturally looking fern however, resembling the Cyclosorus or Thelypteridaceae fern. These are:^[5]^[6]

w	a	b	c	d	e	f	p
ƒ₁	0	0	0	0.25	0	−0.4	0.02
ƒ₂	0.95	0.005	−0.005	0.93	−0.002	0.5	0.84
ƒ₃	0.035	−0.2	0.16	0.04	−0.09	0.02	0.07
ƒ₄	−0.04	0.2	0.16	0.04	0.083	0.12	0.07

References[edit]

^ Jump up to:^a ^b ^c Fractals Everywhere, Boston, MA: Academic Press, 1993, ISBN 0-12-079062-9
^ Jump up to:^a ^b Michael Barnsley, et al.,"V-variable fractals and superfractals" PDF (2.22 MB)
Jump up^ Barnsley, Michael (2000). Fractals everywhere. Morgan Kaufmann. p. 86. ISBN 0-12-079069-6. Retrieved 2010-01-07.
Jump up^ Weisstein, Eric. "Barnsley's Fern". Retrieved 2010-01-07.
Jump up^ Other fern varieties with supplied coefficients, retrieved 2010-1-7
Jump up^ A Barnsley fern generator

漂亮的网页生成该分形的html5工具:

http://www.chradams.co.uk/fern/maker.html

看到Matrix67博客矩阵迭代分形,感觉不错相关推荐

各大高权重搜索引擎博客矩阵链轮？
客营销在现实网络环境中还是有着较大的作用,搜索引擎对博客的收录也是较快的.在百度收录新站小技巧和新站外链建设文章中,陈迪均提到利用目前比较高权重的博客创造外链,新站都不好找外链,好好利用这些博客,虽然 ...
博客属性10个非常不错的CSS技巧
这几周个人几篇文章介绍了改博客属性的文章. 关联文章的地址在这里,妙巧的运用CSS的技能,可以让你不必修改HTML能就失掉很好的博客或者模板表面.我收集了一些非常用有的CSS技能让我们计设博客时更炫 ...
今天逛博客时看到一篇不错的C语言知识点总结，借来看看
总体上必须清楚的: 1)程序结构是三种: 顺序结构 .选择结构(分支结构).循环结构. 2)读程序都要从main()入口, 然后从最上面顺序往下读(碰到循环做循环,碰到选择做选择),有且只有一个ma ...
自媒体博客pc版转成手机版的三种方法
现在做自媒体博客的朋友有很多,可是,大家的自媒体博客都是PC版,只适用于电脑,平板上面,对于手机来说的话就不适合了,影响用户体验.下面,小编就教大家三种方法把自媒体博客PC版转换成手机版网站. 前段时 ...
为什么你写博客时感觉很困难？
沉默王二@了之作品[格物致知.修身齐家] 为什么写博客时感觉很困难?因为准备功夫没做到家呗. 咱们这里说的准备功夫,不是指在打开电脑准备写博客时上百度搜几张图片.到今日头条看看时事热点.到微信订阅号上 ...
博客推广优化SEO排名方案大汇总！何必东奔西走这里的博客优化的文章应有尽有！！...
企业博客优化推广精品方案很有深度,很有参考价值．建立博客群博客地址: ①Donews :http://blog.donews.com/default.html ②新浪:http://blog.s ...
如何高效的利用博客园？
写在前面在河南工作那会儿,虽然遇到问题也百度过,google过,但是很少留意内容来自哪个网站,也许是工作的内容太简单了,也许是太单调了,之后的之后就很少上网查东西了,因为模块相似,功能相似,代码写了 ...
看了《为什么你应该写博客》有感
这一段实在太忙,没有时间写些自己的东西,不过学了不少东西,有技术方面的,也有心得方面的,感到还是受益匪浅的. 最近查看了微软的msdn,感到英语提高了些,不过还是需要继续努力.技术上对c语言更加熟悉了 ...
如何从现在开始写博客？
在前不久知名博主<纯洁的微笑>在博客园分享了他写博客的心得,获得了读者圈的广泛共鸣,同时也引起了一些老生常谈的争议,这样的讨论在我们长沙.NET技术社区内部也经常发生. 1.写博客的好处 ...

看到Matrix67博客矩阵迭代分形,感觉不错