勾股定理

圓

圓形的概念的形成，是人類認知歷史上的一大里程碑。

圓周率

定义1

一个圆形的周长与直径之比：

定义2

以圆形半径为边长作一正方形，然後把圆形面积和此正方形面积比。

定义3

满足

的最小正实数。

这里的正弦函数定义为幂级数

百度百科：圆周率

随着能量的增加，从变分解的极限公式里，哈根和弗里德曼找到了沃利斯的圆周率公式。

量子力学理论在20世纪初期诞生，而沃利斯圆周率公式已经存在了数百年，但这两者之间的内在关联直到今天才被发现。

代数

π是个无理数，即不可表达成两个整数之比，是由瑞士科学家约翰·海因里希·兰伯特于1761年证明的。 1882年，林德曼（Ferdinand von Lindemann）更证明了π是超越数，即π不可能是任何整系数多项式的根。

圆周率的超越性否定了化圆为方这古老尺规作图问题的可能性，因所有尺规作图只能得出代数数，而超越数不是代数数。

数学分析

Leibniz定理：

Wallis公式：

高斯积分：

A graph of the Gaussian function

The colored region between the function and the x-axis has area √π.

斯特林公式：

π的连分数表示：

数论

两个任意自然数是互质的概率是

任取一个任意整数，该整数没有重复质因子的概率为

一个任意整数平均可用

个方法写成两个完全数之和。

概率论

设我们有一个以平行且等距木纹铺成的地板，随意抛一支长度比木纹之间距离小的针，求针和其中一条木纹相交的概率。这就是布丰投针问题。1777 年，布丰自己解决了这个问题——这个概率值是 1/π。

统计学

正态分布的概率密度函数：

圆的内接正多边形和外接正多边形

古希腊大数学家阿基米德(公元前287–212 年) 开创了人类历史上通过理论计算圆周率近似值的先河。阿基米德从单位圆出发，先用内接正六边形求出圆周率的下界为3，再用外接正六边形并借助勾股定理求出圆周率的上界小于4。接着，他对内接正六边形和外接正六边形的边数分别加倍，将它们分别变成内接正12边形和外接正12边形，再借助勾股定理改进圆周率的下界和上界。他逐步对内接正多边形和外接正多边形的边数加倍，直到内接正96边形和外接正96边形为止。最后，他求出圆周率的下界和上界分别为223/71 和22/7， 并取它们的平均值3.141851 为圆周率的近似值。阿基米德用到了迭代算法和两侧数值逼近的概念，称得上是“计算数学”的鼻祖。

公元263年，中国数学家刘徽用“割圆术”计算圆周率，他先从圆内接正六边形，逐次分割一直算到圆内接正192边形。他说“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”，包含了求极限的思想。刘徽给出π=3.141024的圆周率近似值，刘徽在得圆周率=3.14之后，将这个数值和晋武库中汉王莽时代制造的铜制体积度量衡标准嘉量斛的直径和容积检验，发现3.14这个数值还是偏小。于是继续割圆到1536边形，求出3072边形的面积，得到令自己满意的圆周率

公元480年左右，南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果，给出不足近似值3.1415926和过剩近似值3.1415927，还得到两个近似分数值，密率

和约率

歐拉公式

欧拉公式：

Euler's formula states that, for any [real number]


![](http://latex.codecogs.com/svg.latex?e^{ix}=\cos x+i\sin x)

where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively, with the argument x given in radians.

三角函數分析

微積分

使用微积分，我们将圆象洋葱一样分为薄圆环，递增地求出面积。

对“洋葱”，以 t 为半径的无穷薄圆环，贡献的面积是 2πt dt，周长的长度乘以其无穷小宽度。这样对半径为 r 的圆给出了一个初等积分：

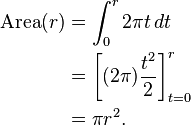
宇宙運行軌道

萬有引力定律

電磁場方程

相對論

相对论的场方程：

量子力學

海森堡不确定性原理：

本文绘图使用：http://zh.numberempire.com/graphingcalculator.php，在次感谢作者！