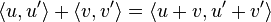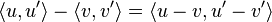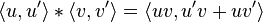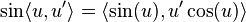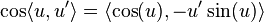Automatic differentiation
看算法看到这个了,转载一下,备忘。
In mathematics and computer algebra, automatic differentiation (AD), also called algorithmic differentiation or computational differentiation,[1][2] is a set of techniques to numerically evaluate the derivative of a function specified by a computer program. AD exploits the fact that every computer program, no matter how complicated, executes a sequence of elementary arithmetic operations (addition, subtraction, multiplication, division, etc.) and elementary functions (exp, log, sin, cos, etc.). By applying the chain rule repeatedly to these operations, derivatives of arbitrary order can be computed automatically, and accurate to working precision.
Automatic differentiation is not:


Figure 1: How automatic differentiation relates to symbolic differentiation
- Symbolic differentiation, or
- Numerical differentiation (the method of finite differences).
These classical methods run into problems: symbolic differentiation works at low speed, and faces the difficulty of converting a computer program into a single expression, while numerical differentiation can introduce round-off errors in the discretization process and cancellation. Both classical methods have problems with calculating higher derivatives, where the complexity and errors increase. Finally, both classical methods are slow at computing the partial derivatives of a function with respect to many inputs, as is needed for gradient-based optimization algorithms. Automatic differentiation solves all of these problems.
Contents
|
The chain rule, forward and reverse accumulation
Fundamental to AD is the decomposition of differentials provided by the chain rule. For the simple composition  the chain rule gives
the chain rule gives
Usually, two distinct modes of AD are presented, forward accumulation (or forward mode) and reverse accumulation (or reverse mode). Forward accumulation specifies that one traverses the chain rule from right to left (that is, first one computes  and then
and then  ), while reverse accumulation has the traversal from left to right.
), while reverse accumulation has the traversal from left to right.
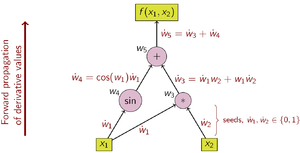

Figure 2: Example of forward accumulation with computational graph
Forward accumulation
Forward accumulation automatic differentiation is the easiest to understand and to implement. The function  is interpreted (by a computer or human programmer) as the sequence of elementary operations on the work variables
is interpreted (by a computer or human programmer) as the sequence of elementary operations on the work variables 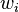 , and an AD tool for forward accumulation adds the corresponding operations on the second component of the augmented arithmetic.
, and an AD tool for forward accumulation adds the corresponding operations on the second component of the augmented arithmetic.
| Original code statements | Added statements for derivatives |
|---|---|
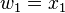
|
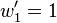 (seed) (seed)
|

|
 (seed) (seed)
|

|
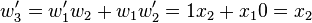
|

|

|
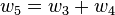
|

|
The derivative computation for  needs to be seeded in order to distinguish between the derivative with respect to
needs to be seeded in order to distinguish between the derivative with respect to  or
or 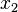 . The table above seeds the computation with
. The table above seeds the computation with 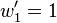 and
and  and we see that this results in
and we see that this results in  which is the derivative with respect to
which is the derivative with respect to  . Note that although the table displays the symbolic derivative, in the computer it is always the evaluated (numeric) value that is stored. Figure 2 represents the above statements in a computational graph.
. Note that although the table displays the symbolic derivative, in the computer it is always the evaluated (numeric) value that is stored. Figure 2 represents the above statements in a computational graph.
In order to compute the gradient of this example function, that is  and
and 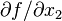 , two sweeps over the computational graph is needed, first with the seeds
, two sweeps over the computational graph is needed, first with the seeds 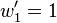 and
and  , then with
, then with  and
and  .
.
The computational complexity of one sweep of forward accumulation is proportional to the complexity of the original code.
Forward accumulation is superior to reverse accumulation for functions  with
with  as only one sweep is necessary, compared to
as only one sweep is necessary, compared to  sweeps for reverse accumulation.
sweeps for reverse accumulation.
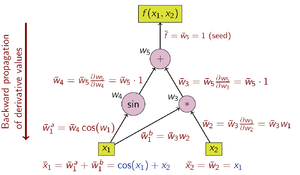

Figure 3: Example of reverse accumulation with computational graph
Reverse accumulation
Reverse accumulation traverses the chain rule from left to right, or in the case of the computational graph in Figure 3, from top to bottom. The example function is real-valued, and thus there is only one seed for the derivative computation, and only one sweep of the computational graph is needed in order to calculate the (two-component) gradient. This is only half the work when compared to forward accumulation, but reverse accumulation requires the storage of some of the work variables 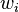 , which may represent a significant memory issue.
, which may represent a significant memory issue.
The data flow graph of a computation can be manipulated to calculate the gradient of its original calculation. This is done by adding an adjoint node for each primal node, connected by adjoint edges which parallel the primal edges but flow in the opposite direction. The nodes in the adjoint graph represent multiplication by the derivatives of the functions calculated by the nodes in the primal. For instance, addition in the primal causes fanout in the adjoint; fanout in the primal causes addition in the adjoint; a unary function 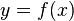 in the primal causes
in the primal causes 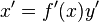 in the adjoint; etc.
in the adjoint; etc.
Reverse accumulation is superior to forward accumulation for functions 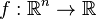 with
with 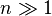 , where forward accumulation requires roughly n times as much work.
, where forward accumulation requires roughly n times as much work.
Backpropagation of errors in multilayer perceptrons, a technique used in machine learning, is a special case of reverse mode AD.
Jacobian computation
The Jacobian  of
of  is an
is an 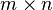 matrix. The Jacobian can be computed using
matrix. The Jacobian can be computed using  sweeps of forward accumulation, of which each sweep can yield a column vector of the Jacobian, or with
sweeps of forward accumulation, of which each sweep can yield a column vector of the Jacobian, or with  sweeps of reverse accumulation, of which each sweep can yield a row vector of the Jacobian.
sweeps of reverse accumulation, of which each sweep can yield a row vector of the Jacobian.
Beyond forward and reverse accumulation
Forward and reverse accumulation are just two (extreme) ways of traversing the chain rule. The problem of computing a full Jacobian of  with a minimum number of arithmetic operations is known as the "optimal Jacobian accumulation" (OJA) problem. OJA is NP-complete.[3] Central to this proof is the idea that there may exist algebraic dependences between the local partials that label the edges of the graph. In particular, two or more edge labels may be recognized as equal. The complexity of the problem is still open if it is assumed that all edge labels are unique and algebraically independent.
with a minimum number of arithmetic operations is known as the "optimal Jacobian accumulation" (OJA) problem. OJA is NP-complete.[3] Central to this proof is the idea that there may exist algebraic dependences between the local partials that label the edges of the graph. In particular, two or more edge labels may be recognized as equal. The complexity of the problem is still open if it is assumed that all edge labels are unique and algebraically independent.
Automatic differentiation using dual numbers
Forward mode automatic differentiation is accomplished by augmenting the algebra of real numbers and obtaining a new arithmetic. An additional component is added to every number which will represent the derivative of a function at the number, and all arithmetic operators are extended for the augmented algebra. The augmented algebra is the algebra of dual numbers. Computer programs often implement this using the complex number representation.
Replace every number 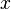 with the number
with the number  , where
, where 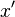 is a real number, but
is a real number, but  is nothing but a symbol with the property
is nothing but a symbol with the property  . Using only this, we get for the regular arithmetic
. Using only this, we get for the regular arithmetic
and likewise for subtraction and division.
Now, we may calculate polynomials in this augmented arithmetic. If  , then
, then

|

|

|

|
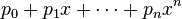
|
|

|
||

|
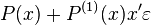
|
where 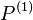 denotes the derivative of
denotes the derivative of 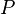 with respect to its first argument, and
with respect to its first argument, and 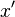 , called a seed, can be chosen arbitrarily.
, called a seed, can be chosen arbitrarily.
The new arithmetic consists of ordered pairs, elements written  , with ordinary arithmetics on the first component, and first order differentiation arithmetic on the second component, as described above. Extending the above results on polynomials to analytic functions we obtain a list of the basic arithmetic and some standard functions for the new arithmetic:
, with ordinary arithmetics on the first component, and first order differentiation arithmetic on the second component, as described above. Extending the above results on polynomials to analytic functions we obtain a list of the basic arithmetic and some standard functions for the new arithmetic:
and in general for the primitive function  ,
,
where 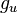 and
and 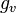 are the derivatives of
are the derivatives of  with respect to its first and second arguments, respectively.
with respect to its first and second arguments, respectively.
When a binary basic arithmetic operation is applied to mixed arguments—the pair  and the real number
and the real number  —the real number is first lifted to
—the real number is first lifted to  . The derivative of a function
. The derivative of a function 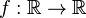 at the point
at the point  is now found by calculating
is now found by calculating  using the above arithmetic, which gives
using the above arithmetic, which gives  as the result.
as the result.
Vector arguments and functions
Multivariate functions can be handled with the same efficiency and mechanisms as univariate functions by adopting a directional derivative operator, which finds the directional derivative  of
of  at
at 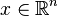 in the direction
in the direction  by calculating
by calculating 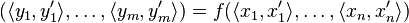 using the same arithmetic as above.
using the same arithmetic as above.
Higher order differentials
The above arithmetic can be generalized, in the natural way, to calculate parts of the second order and higher derivatives. However, the arithmetic rules quickly grow very complicated: complexity will be quadratic in the highest derivative degree. Instead, truncated Taylor series arithmetic is used. This is possible because the Taylor summands in a Taylor series of a function are products of known coefficients and derivatives of the function. Currently, there exists efficient Hessian automatic differentiation methods that calculate the entire Hessian matrix with a single forward and reverse accumulation. There also exist a number of specialized methods for calculating large sparse Hessian matrices.
Implementation
Forward-mode AD is implemented by a nonstandard interpretation of the program in which real numbers are replaced by dual numbers, constants are lifted to dual numbers with a zero epsilon coefficient, and the numeric primitives are lifted to operate on dual numbers. This nonstandard interpretation is generally implemented using one of two strategies: source code transformation or operator overloading.
Source code transformation (SCT)


Figure 4: Example of how source code transformation could work
The source code for a function is replaced by an automatically generated source code that includes statements for calculating the derivatives interleaved with the original instructions.
Source code transformation can be implemented for all programming languages, and it is also easier for the compiler to do compile time optimizations. However, the implementation of the AD tool itself is more difficult.
Operator overloading (OO)


Figure 5: Example of how operator overloading could work
Operator overloading is a possibility for source code written in a language supporting it. Objects for real numbers and elementary mathematical operations must be overloaded to cater for the augmented arithmetic depicted above. This requires no change in the form or sequence of operations in the original source code for the function to be differentiated, but often requires changes in basic data types for numbers and vectors to support overloading and often also involves the insertion of special flagging operations.
Operator overloading for forward accumulation is easy to implement, and also possible for reverse accumulation. However, current compilers lag behind in optimizing the code when compared to forward accumulation.
Software
- C/C++
-
Package License Approach Brief Info ADC Version 4.0 nonfree OO ADIC free for noncommercial SCT forward mode ADMB BSD SCT+OO ADNumber dual license OO arbitrary order forward/reverse ADOL-C CPL 1.0 or GPL 2.0 OO arbitrary order forward/reverse, part of COIN-OR AMPL free for students SCT FADBAD++ free for
noncommercialOO uses operator new CasADi LGPL OO/SCT Forward/reverse modes, matrix-valued atomic operations. ceres-solver BSD OO A portable C++ library that allows for modeling and solving large complicated nonlinear least squares problems CppAD EPL 1.0 or GPL 3.0 OO arbitrary order forward/reverse, AD<Base> for arbitrary Base including AD<Other_Base>, part of COIN-OR; can also be used to produce C source code using the CppADCodeGen library. OpenAD depends on components SCT Sacado GNU GPL OO A part of the Trilinos collection, forward/reverse modes. Stan BSD OO Estimates Bayesian statistical models using Hamiltonian Monte Carlo. TAPENADE Free for noncommercial SCT CTaylor free OO truncated taylor series, multi variable, high performance, calculating and storing only potentially nonzero derivatives, calculates higher order derivatives, order of derivatives increases when using matching operations until maximum order (parameter) is reached, example source code and executable available for testing performance
- Fortran
-
Package License Approach Brief Info ADF Version 4.0 nonfree OO ADIFOR >>>
(free for non-commercial)SCT AUTO_DERIV free for non-commercial OO OpenAD depends on components SCT TAPENADE Free for noncommercial SCT
- Matlab
-
Package License Approach Brief Info AD for MATLAB GNU GPL OO Forward (1st & 2nd derivative, Uses MEX files & Windows DLLs) Adiff BSD OO Forward (1st derivative) MAD Proprietary OO ADiMat ? SCT Forward (1st & 2nd derivative) & Reverse (1st)
- Python
-
Package License Approach Brief Info ad BSD OO first and second-order, reverse accumulation, transparent on-the-fly calculations, basic NumPy support, written in pure python FuncDesigner BSD OO uses NumPy arrays and SciPy sparse matrices,
also allows to solve linear/non-linear/ODE systems and
to perform numerical optimizations by OpenOptScientificPython CeCILL OO see modules Scientific.Functions.FirstDerivatives and
Scientific.Functions.Derivativespycppad BSD OO arbitrary order forward/reverse, implemented as wrapper for CppAD including AD<double> and AD< AD<double> >. pyadolc BSD OO wrapper for ADOL-C, hence arbitrary order derivatives in the (combined) forward/reverse mode of AD, supports sparsity pattern propagation and sparse derivative computations uncertainties BSD OO first-order derivatives, reverse mode, transparent calculations algopy BSD OO same approach as pyadolc and thus compatible, support to differentiate through numerical linear algebra functions like the matrix-matrix product, solution of linear systems, QR and Cholesky decomposition, etc. pyderiv GNU GPL OO automatic differentiation and (co)variance calculation CasADi LGPL OO/SCT Python front-end to CasADi. Forward/reverse modes, matrix-valued atomic operations.
- .NET
| Package | License | Approach | Brief Info |
|---|---|---|---|
| AutoDiff | GNU GPL | OO | Automatic differentiation with C# operators overloading. |
| FuncLib | MIT | OO | Automatic differentiation and numerical optimization, operator overloading, unlimited order of differentiation, compilation to IL code for very fast evaluation. |
- Haskell
| Package | License | Approach | Brief Info |
|---|---|---|---|
| ad | BSD | OO |
Forward Mode (1st derivative or arbitrary order derivatives via lazy lists and sparse tries) Reverse Mode Combined forward-on-reverse Hessians. Uses Quantification to allow the implementation automatically choose appropriate modes. Quantification prevents perturbation/sensitivity confusion at compile time. |
| fad | BSD | OO | Forward Mode (lazy list). Quantification prevents perturbation confusion at compile time. |
| rad | BSD | OO |
Reverse Mode. (Subsumed by 'ad'). Quantification prevents sensitivity confusion at compile time. |
- Octave
| Package | License | Approach | Brief Info |
|---|---|---|---|
| CasADi | LGPL | OO/SCT | Octave front-end to CasADi. Forward/reverse modes, matrix-valued atomic operations. |
- Java
| Package | License | Approach | Brief Info |
|---|---|---|---|
| JAutoDiff | - | OO | Provides a framework to compute derivatives of functions on arbitrary types of field using generics. Coded in 100% pure Java. |
| Apache Commons Math | Apache License v2 | OO | This class is an implementation of the extension to Rall's numbers described in Dan Kalman's paper[4] |
References
- ^ Neidinger, Richard D. (2010). "Introduction to Automatic Differentiation and MATLAB Object-Oriented Programming". SIAM Review 52 (3): 545–563.
- ^ http://www.ec-securehost.com/SIAM/SE24.html
- ^ Naumann, Uwe (April 2008). Optimal Jacobian accumulation is NP-complete. "Optimal Jacobian accumulation is NP-complete". Mathematical Programming 112 (2): 427–441. doi:10.1007/s10107-006-0042-z
- ^ Kalman, Dan (June 2002). "Doubly Recursive Multivariate Automatic Differentiation". Mathematics Magazine 75 (3): 187–202.
Literature
- Rall, Louis B. (1981). Automatic Differentiation: Techniques and Applications. Lecture Notes in Computer Science 120. Springer. ISBN 3-540-10861-0.
- Griewank, Andreas; Walther, Andrea (2008). Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation. Other Titles in Applied Mathematics 105 (2nd ed.). SIAM. ISBN 978-0-89871-659-7.
- Neidinger, Richard (2010). "Introduction to Automatic Differentiation and MATLAB Object-Oriented Programming". SIAM Review 52 (3): 545–563. doi:10.1137/080743627. Retrieved 2013-03-15.
External links
- www.autodiff.org, An "entry site to everything you want to know about automatic differentiation"
- Automatic Differentiation of Parallel OpenMP Programs
- Automatic Differentiation, C++ Templates and Photogrammetry
- Automatic Differentiation, Operator Overloading Approach
- Compute analytic derivatives of any Fortran77, Fortran95, or C program through a web-based interface Automatic Differentiation of Fortran programs
- Description and example code for forward Automatic Differentiation in Scala
- Adjoint Algorithmic Differentiation: Calibration and Implicit Function Theorem
Automatic differentiation相关推荐
- arguments don‘t support automatic differentiation, but one of the arguments
pytorch报错:Index_select(): functions with out=- arguments don't support automatic differentiation 解决: ...
- 自动微分(Automatic Differentiation)
目录 什么是自动微分 手动求解法 数值微分法 符号微分法 自动微分法 自动微分Forward Mode 自动微分Reverse Mode 参考引用 现代深度学习系统中(比如MXNet, TensorF ...
- 谈谈自动微分(Automatic Differentiation)
©作者 | JermyLu 学校 | 中国科学院大学 研究方向 | 自然语言处理与芯片验证 引言 众所周知,Tensorflow.Pytorch 这样的深度学习框架能够火起来,与其包含自动微分机制有着 ...
- 计算机求导方法:自动微分(Automatic Differentiation)
目录 1 Manual Differentiation (手动微分) 1.1 计算方法 1.2 缺陷 2 Symbolic Differentiation (符号微分) 2.1 计算方法 2.2 缺陷 ...
- Automatic differentiation in PyTorch
文章阅读 Automatic differentiation in PyTorch 主要内容 Pytorch是一个深度学习框架,提供了高性能的环境以及容易使用的自动微分模块,并能在不同设备上运行 Py ...
- 如何在python中表示微分_Python实现自动微分(Automatic Differentiation)
什么是自动微分 自动微分(Automatic Differentiation)是什么?微分是函数在某一处的导数值,自动微分就是使用计算机程序自动求解函数在某一处的导数值.自动微分可用于计算神经网络反向 ...
- PyTorch随笔 - Automatic Differentiation 自动微分
面试题: 函数:f(1) = x, f(n+1) = 4*f(n)*(1-f(n)) 实现f(4)的函数,当x=2时,f(4)的值是多少,导数(微分)值是多少? 即: def func(x, k):. ...
- 自动微分(Automatic Differentiation)简介
现代深度学习系统中(比如MXNet, TensorFlow等)都用到了一种技术--自动微分.在此之前,机器学习社区中很少发挥这个利器,一般都是用Backpropagation进行梯度求解,然后进行SG ...
- 详解自动微分(Automatic Differentiation)
©作者 | JermyLu 编辑 paperweekly 学校 | 中国科学院大学 研究方向 | 自然语言处理与芯片验证 引言 众所周知,Tensorflow.Pytorch 这样的深度学习框架能够 ...
最新文章
- 编写单元测试代码遵守BCDE原则,以保证被测试模块的交付质量,那么下列说法正确的是
- 体验首款Linux消费级平板,原来芯片和系统全是国产
- 云原生收购潮:思科计划收购Portshift;Kasten加入Veeam
- 初始化列表||类对象作为类成员|| 静态成员
- MYSQL中的主表和父表_主表,从表,关联表,父表,子表
- html 实现表格控制器,HTML 表格类 - CodeIgniter 2.x 用户手册
- 【实时+排重】摆脱渠道统计刷量作弊行为
- PhpSpreadsheet 电子表格(excel) PHP处理笔记
- OpenNI2 + NiTE2开发教程
- 实现一个基于Vue的Button小组件
- 【caffe-windows】 caffe-master 之 mnist 超详细
- cd如何省略空格 linux_在 Linux 上调整命令历史 | Linux 中国
- div垂直居中的几种方法
- 独到理解@java数据类型
- openssl 1.0.2k-fips 升级到 openssl-3.0.5
- c语言中单链表的逆置
- 计算机专业男生好撩吗,撩男生很甜很撩的句子 一撩一个准
- pytest-mian函数运行
- [4G5G基础学习]:流程 - 4G LTE 接入网的随机接入流程
- 字符串匹配KMP算法讲解