22计算机408考研—数据结构—图
手把手教学考研大纲范围内图的存储和遍历 22考研大纲数据结构要求的是C/C++,笔者以前使用的都是Java,对于C++还很欠缺,
如有什么建议或者不足欢迎大佬评论区或者私信指出 初心是用最简单的语言描述数据结构
Talk is cheap. Show me the code.
理论到处都有,代码加例题自己练习才能真的学会
一、图的基本概念
二、图的存储结构
2.1、邻接矩阵
2.2、邻接表
2.3、十字链表
2.4、邻接多重表
三、图的遍历
3.1、深度优先搜索
3.2、广度优先搜索
3.3、Dijkstra最短路径
3.4、Floyd最短路径
3.5、Prim最短路径
一、图的基本概念
图
官方解释:图G由集合V和集合E组成,记作G = (V,E)V(G)代表图G的顶点集合 (有穷非空集合)E(G)代表图G的边集合(如果图G为空,则图只有顶点没有边)
歪理:树是一个结点对应多个结点,图就是多个结点对应多个结点图可以想象成一个乱七八糟的树线性表和树都可以看作是一种特殊的图
图分为有向图和无向图
1、有向图:
顾名思义,有向图是有方向的图
1->2 但是 2不能指向1

2、无向图:
没有方向的图
只要有边存在就可以互相走,a -> c , c -> a 两种都存在

3、子图:
官方解释:
G = (V,E)和G' = (V', E')
V'属于V, E'属于E
称G'为G的子图

当前图的子图有:
1 -> 2
1 -> 2 -> 4
3 -> 4
等等很多,无向图也是一样的
4、完全图:
对于无向图:
若具有n(n-1)条边,则称为无向完全图。
对于有向图:
若具有n(n-1)条边,则称为有向完全图。
5、稀疏图和稠密图:
边的数量相对顶点很少的图称为稀疏图,反之称为稠密图。
6、权和网:
在一些情况下,每条边可以标上具有某种含义的数值,该数值称为该边上的权。
这些权表示从 一个顶点到另一个顶点 的距离或者耗费,这种带权的图通常称为网。
7、邻接点:
对于无向图G,如果图的边(a,b)属于 E ,则称 a,b 互为邻接点,即 a,b 相邻接,边(a,b)依附于顶点 a 和 b ,边(a,b)与顶点a,b相关联。
8、度,入度和出度:
顶点 v 的度是:与 v 相关联的边的数目,记作 TD(v) 。
对于有向图,顶点 v 的度分为入度和出度:
入度是指向 v 的边的数目,记为 ID(v) 。
出度是从 v 指出来的边的数目,记作 OD(v) 。
例子:

以顶点 2 为例子:
顶点 2 的入度ID(v)= 1
顶点 2 的出度OD(v)= 2
顶点 2 的度为TD(v)= ID(v)+ OD(v)= 3
边和度之间的关系:
顶点 vi 的度记为 TD(v),那么一个有 n 个顶点,e 条边的图,满足如下关系
e = (TD(v1) + TD(v2) + …… +TD(vn))/ 2
7、路径和路径长度:
顶点 Va 到顶点 Vb 之间的 路径: 是指顶点序列 {Va,Vi1,Vi2,……,Vim,Vb}
路径长度: 路径中边的数目
回路或环: 第一个顶点和最后一个顶点 相同的路径 称为回路或环(也就是 a 和 b 相同)
简单路径: 路径中顶点不重复出现的路径的路径为简单路径
简单回路 或 简单环: 除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路,称为简单回路 或 简单环
8、连通、连通图和连通分量:
在无向图中
如果从顶点 A 到顶点 B 有路径,则称 A 和 B 是 连通 的
如果图中任意两个两个顶点 A ,B 都是连通的,则称图为 连通图
在无向图中
上图不是连通图
下面是上图的三个连通分量
连通分量也称作无向图中的极大连通子图
也就是说,把一个非连通图完全分成多个连通图,这些连通图就叫做连通分量
9、强连通图和强连通分量:

在有向图中 如果图中任意两个两个顶点 A ,B 都是连通的,则称图为 强连通图

在有向图中: G4不是强连通图,但是他有三个强连通分量
10、连通图的生成树、有向树和生成森林:
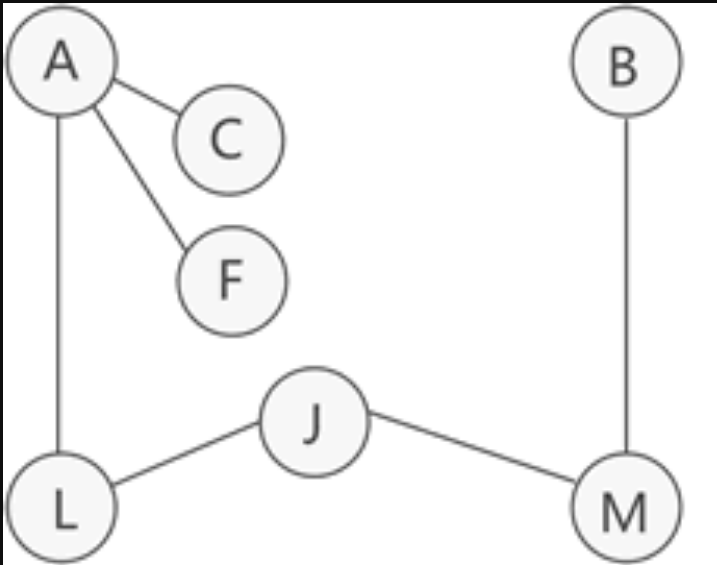
**连通图的生成树:**是包含图中全部顶点的一个极小连通子图。若图中顶点数为 n ,则它的生成树含有 n − 1 条边。
对生成树而言,若砍去一条边,则会变成非连通图
若加上一条边则会形成一个回路。
在非连通图中,连通分量的生成树构成了非连通图的生成森林

有向树: 有一个顶点的入度为0,其余顶点的入度均为1的有向图称为有向树
换句话说,一个有向图的生成森林是由若干棵有向树组成。
二、图的存储结构
图的结构相对于其他来说比较复杂,任何两个顶点之间都可能存在联系,无法用顺序存储的方式存储图之间的关系(无法用一维数组来保存图)
虽然图无法用顺序存储的方式,但是可以用二维数组的方式表示元素之间的关系,即 邻接矩阵 表示法。
由于图的任意两个结点都可能存在关系,用链式存储图也很常见。
图的链式存储有:邻接表、十字链表和邻接多重表。(应该根据实际需要选择不通的存储结构)
2.1、邻接矩阵
邻接矩阵: 顶点之间相邻关系的矩阵。
图
图G(V,E)是具有 n 个顶点的图(A[ i,j] = 1表示顶点 i 和顶点 j 有一条边联系,反之则没有边联系)


**对角线上的都是0:**都是对应当前点(V0,V0 V1,V1 ……)顶点是无法自身与自身相连接的
对于无向图来说,其实他们是关于对角线对称的( i 与j相连,那么j与i肯定也是相连的)
对于有向图来说,没有这个规律 ( i 与j相连,那么j与i不一定相连)
网
网G,邻接矩阵可以定义为如下(其实和图是一样的,不过就是把顶点有关系变成了顶点直接的权值)
A[ i,j] = 3 表示顶点 i 和顶点 j 有一条边,边的权值为3


和图一样,对角线上一定为0,顶点无法与自身相连接
邻接矩阵示例代码
代码:
(无向图也可以这么创建,无向图就不需要输入权值了,把相关联的两个点在矩阵中置1)
#include <iostream>using namespace std;#define None 0 //顶点之间没有关系用0表示
#define MAXNum 100 //设图中顶点数量最多为100typedef struct { //图的结构体:顶点列表,邻接矩阵,图的点数和边数int nodes[MAXNum];int arcs[MAXNum][MAXNum];int vewnum, arcnum;
} AMGraph;//取顶点在顶点表中的下标
int getAMGraphIndex(AMGraph G, int node) {for (int i = 0; i < G.vewnum; i++) { //循环顶点表,找到顶点,返回下标if (G.nodes[i] == node) {return i;}}return -1;
}//邻接矩阵法创建无向图
bool createAMGraph (AMGraph &G) {cout << "请输入顶点数量和边的数量" << endl;cin >> G.vewnum >> G.arcnum; //输入 顶点数 和 边数for (int i = 0; i < G.vewnum; i++) { //输入顶点cout << "请输入顶点的值" << endl;cin >> G.nodes[i];}for (int i = 0; i < G.vewnum; i++) { //邻接矩阵,初始化顶点间的边(关系)都为空for (int j = 0; j < G.vewnum; j++) {G.arcs[i][j] = None;}}int v1, v2, w;int i1, i2;for (int i = 0; i < G.arcnum; i++) { //接收两个顶点和顶点间边的权值cout << "请输入新建边相邻的两个结点,以及这条边的权重" << endl;cin >> v1 >> v2 >> w;i1 = getAMGraphIndex(G, v1); //找到两个顶点的下标i2 = getAMGraphIndex(G, v2);G.arcs[i1][i2] = G.arcs[i2][i1] = w; //在邻接矩阵中建立关系}return true;
}//输出图
void printAMGraph(AMGraph G) {cout << "顶点数:" << G.vewnum << "边数:" << G.arcnum << "\n";cout << "顶点表:";for (int i = 0; i < G.vewnum; i++) {cout << G.nodes[i] << " ";}cout << "\n";cout << "邻接矩阵关系(A[i,j] = 3 表示顶点 i 和顶点 j 有一条边,边的权值为3):\n";for (int i = 0; i < G.vewnum; i++) {for (int j = 0; j < G.vewnum; j++) {cout << G.arcs[i][j] << " ";}cout << "\n";}cout << "\n";}int main() {AMGraph G;//输入例子//5 6 1 2 3 4 5 1 5 8 1 3 6 1 4 9 2 3 8 5 4 9 3 4 6createAMGraph(G);printAMGraph(G);return 0;
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
请输入顶点数量和边的数量
5 6
请输入顶点的值
1
请输入顶点的值
2
请输入顶点的值
3
请输入顶点的值
4
请输入顶点的值
5
请输入新建边相邻的两个结点,以及这条边的权重
1 5 8
请输入新建边相邻的两个结点,以及这条边的权重
1 3 6
请输入新建边相邻的两个结点,以及这条边的权重
1 4 9
请输入新建边相邻的两个结点,以及这条边的权重
2 3 8
请输入新建边相邻的两个结点,以及这条边的权重
5 4 9
请输入新建边相邻的两个结点,以及这条边的权重
3 4 6
顶点数:5边数:6
顶点表:1 2 3 4 5
邻接矩阵关系(A[i,j] = 3 表示顶点 i 和顶点 j 有一条边,边的权值为3):
0 0 6 9 8
0 0 8 0 0
6 8 0 6 0
9 0 6 0 9
8 0 0 9 0 Process finished with exit code 02.2、邻接表
当一个图中,边的数量少 时(也叫做稀疏图),用邻接矩阵会很 浪费空间 ,这时候 邻接表 就出来了

邻接表结构:

头结点包含一个 顶点 和一个指向 边(表结点) 的指针
表结点包含一个 顶点 ,一个指向 下一条边(表结点) 的指针 和 边的权值(图没有权值)
Tips: 这里指向的边,都是 以当前 头结点 顶点 直接联系 的边
eg:
比如这个以 V1 直接联系的点是 V4 和 V2 ,所以表结点是 V4 和 V2
无向图

有向图

解释:
0-4 代表 a-e
邻接矩阵中,是以顶点为起点的关系(逆邻接矩阵,以顶点为终点的关系)
0 -> 1 (a->b) 的边,权重 e1
0 -> 2 (a->c) 的边,权重 e2
0没有指向其他方向的边了
多分析分析这几个图,其实很容易懂得
邻接表示例代码
代码:
#include "iostream"using namespace std;#define MAXNum 100 //顶点数最大为100typedef struct ArcNode { //定义边结点结构体:顶点的邻点adjvex,边的权重,下一个边结点的指针int adjvex;int info;struct ArcNode *nextarc;
} ArcNode;typedef struct VNode { //定义表头结点结构体:顶点data,指向边结点的指针int data;ArcNode *firstarc;
} VNode, AdjList[MAXNum]; //AdjList 是表头结点的数组类型typedef struct { //定义邻接表结构体:表头结点数组,顶点数量和边数量AdjList vertices;int vexnum, arcnum;
} ALGraph;//找到顶点在表头结点的下标
int getGraphIndex(ALGraph G, int targetnode) {for (int i = 0; i < G.vexnum; i++) {if (G.vertices[i].data == targetnode) {return i;}}return -1;
}//创建邻接表
bool createGraph(ALGraph &G) {cout << "请输入顶点数量和边的数量" << endl;cin >> G.vexnum >> G.arcnum; //输出顶点数量和边数量for (int i = 0; i < G.vexnum; i++) { //输出顶点,并且设置指向的边结点为空cout << "请输入顶点的值" << endl;cin >> G.vertices[i].data;G.vertices[i].firstarc = NULL;}int v1, v2, i1, i2;for (int i = 0; i < G.arcnum; i++) { //输入两个相邻的顶点cout << "请输入新建边相邻的两个结点" << endl;cin >> v1 >> v2;i1 = getGraphIndex(G, v1); //找到两个顶点的下标i2 = getGraphIndex(G, v2);ArcNode *p1 = new ArcNode; //创建p1边结点,让v1表头结点指向p1边结点p1->adjvex = v2; //p1设置邻接点为v2p1->nextarc = G.vertices[i1].firstarc; //采用头插法,如果采用尾插,每次都要循环到当前表头结点的最后一个末尾边结点才能插入G.vertices[i1].firstarc = p1;ArcNode *p2 = new ArcNode; //与上面同理p2->adjvex = v1;p2->nextarc = G.vertices[i2].firstarc;G.vertices[i2].firstarc = p2;}return true;
}//输出邻接表
void printGraph(ALGraph G) {for (int i = 0; i < G.vexnum; i++) {cout << G.vertices[i].data << " : ";ArcNode *temp = G.vertices[i].firstarc;while (temp != NULL) {cout << "下一个顶点:" << temp->adjvex << " ";temp = temp->nextarc;}cout << "下一个顶点为空\n";}
}int main() {ALGraph G;//输入样例:4 3 1 2 3 4 1 2 1 3 2 3createGraph(G);printGraph(G);
}输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
请输入顶点数量和边的数量
4 3
请输入顶点的值
1
请输入顶点的值
2
请输入顶点的值
3
请输入顶点的值
4
请输入新建边相邻的两个结点
1 2
请输入新建边相邻的两个结点
1 3
请输入新建边相邻的两个结点
2 3
1 : 下一个顶点:3 下一个顶点:2 下一个顶点为空
2 : 下一个顶点:3 下一个顶点:1 下一个顶点为空
3 : 下一个顶点:2 下一个顶点:1 下一个顶点为空
4 : 下一个顶点为空Process finished with exit code 02.3、十字链表
十字链表特点:
十字链表是有向图的另一种链式结构,可以看作邻接表和逆邻接表结合起来得到的一种链表。
十字链表可以快速得到与某点相关联的边,可以高效存取。
大致理解为:每一行第一个为顶点结点,顶点结点的指针根据规律指向对应的边结点。
十字链表结构:

顶点表结点:
data:表示顶点的值
firstin:指向第一个以当前结点为终止点的边(first 第一个 in 进入 第一个进入该结点的边)
firstout:指向第一个以当前结点为起始点的边(first 第一个 out 出去 第一个从该结点出去的边)
边结点:
tailvex:存储边的起始点。(tailvex代表的是弧尾,也就是起始点 A -> B 弧尾是A,这条边从A开始)
headvex:存储边的终止点(headvex 代表的是弧头)
hlink:指向上一条以 headvex 为终止点的边。
tlink:指向上一条以 tailvex 为起始点的边。
十字链表例图:

以 V1 点为例子,
找从V1起始的边:
V1的 firstout(指向第一个以当前结点为起始点的边)指向边 0->1 ,(这里存储的是结点下标)
此边的 tlink (指向和当前边的起始结点相同的上一条边)指向 0->2
可一直通过边的 tlink 找到相同起始点的边
找以 V1 结束的边:
V1 的 firstin (指向第一个以当前结点为终止点的边)指向边 3->0 ,
此边的 hlink (指向和当前边终止结点相同的上一条边) ,不存在终止结点相同上一条边,此时为NULL
可一直通过边的 hlink 找相同终止点的边
十字链表的最大优点:
把邻接表和逆邻接表整合在一起了,很容易找到以 V1 为起始点的边,也容易找到以 V1 为终止点的边。
十字链表示例代码
代码:
#include "iostream"using namespace std;#define MAXSize 100 //顶点数最大为100typedef struct ArcNode { //定义边结点结构体:(边采用头插法)int info; //边的权重,int tailvex; //边的尾结点的下标(一条边的起始点下标)int headvex; //边的头结点的下标(一条边的终止点下标)struct ArcNode *hlink; //指向上一条 与边的头结点相同的边 (指向上一条有相同起始点的边)struct ArcNode *tlink; //指向上一条 与边的尾结点相同的边 (指向上一条有相同终止点的边)
} ArcNode;typedef struct VNode { //定义表头结点结构体:int data; //结点的数据ArcNode *firstin; //指向最后一条以当前顶点为结尾的边(最后一条以当前点的下标为终止点的边)ArcNode *firstout; //指向最后一条以当前顶点为起始的边(最后一条以当前点的下标为起始点的边)
} VexNode;typedef struct { //定义十字链表结构体:表头结点数组,结点数量和边数量VexNode vexlist[MAXSize];int vexnum, arcnum;
} ALGraph;
//找到顶点在表头结点的下标
int getGraphIndex(ALGraph G, int targetnode) { //通过结点的值,找到在图中表头结点的下标(如果不存在,返回-1)for (int i = 0; i < G.vexnum; i++) {if (G.vexlist[i].data == targetnode) {return i;}}return -1;
}//创建边
bool createArc(ALGraph &G) { //(边采用头插法)int vex1, vex2, index1, index2; //起始点,终止点,起始点下标,终止点下标cout << "输入边的起始点和终止点" << endl;cin >> vex1 >> vex2;index1 = getGraphIndex(G, vex1); //找到两个顶点的下标index2 = getGraphIndex(G, vex2);if (index1 == -1 && index2 == -1) {cout << "起始顶点和终止顶点不存在" << endl;return false;} else if (index1 == -1) {cout << "起始顶点不存在" << endl;return false;} else if (index2 == -1) {cout << "终止顶点不存在" << endl;return false;}ArcNode *newArc = new ArcNode; //创建新边结点,新边的起始点指向index1,终止点指向index2newArc->tailvex = index1;newArc->headvex = index2;ArcNode *oldtail = G.vexlist[index1].firstout; //找到当前index1为起始点的第一条边ArcNode *oldhead = G.vexlist[index2].firstin; //找到当前index2为终止点的第一条边newArc->hlink = oldhead; //新边的index2为终止点的边指向oldhead(oldhead就成了上一个以index2为终止点的边)newArc->tlink = oldtail; //新边的index2为起始点的边指向oldtail(oldtail就成了上一个以index2为起始点的边)G.vexlist[index1].firstout = newArc; //以index1为起始点的第一条边指向新边(头插法)G.vexlist[index2].firstin = newArc; //以index2为终止点的第一条边指向新边cout << vex1 << "->" << vex2 << " 创建成功" << endl;return true;
}//删除边
bool deleteArc(ALGraph &G) {int vex1, vex2, index1, index2;cout << "输入边的起始点和终止点" << endl;cin >> vex1 >> vex2;index1 = getGraphIndex(G, vex1);index2 = getGraphIndex(G, vex2);if (index1 == -1 && index2 == -1) {cout << "起始顶点和终止顶点不存在" << endl;return false;} else if (index1 == -1) {cout << "起始顶点不存在" << endl;return false;} else if (index2 == -1) {cout << "终止顶点不存在" << endl;return false;}ArcNode *targetArc;ArcNode *firstOutCur = G.vexlist[index1].firstout; //找到index1为起始点的第一条边ArcNode *firstOutPre;int count = 0;while (firstOutCur) { //看边是否存在count++; //每循环一次就是上一条边,count每次加1,记录这是第几条边//找到起始点和终止点对应的那条边(找到就终止)if (firstOutCur->tailvex == index1 && firstOutCur->headvex == index2) {break;}firstOutPre = firstOutCur; //把当前边给pre,cur指向下一个以index1为起始点的边firstOutCur = firstOutCur->tlink;}if (count == 0 || !firstOutCur) { //count等于0 说明没进循环 firstOutCur为空cout << "不存在该边" << endl; //或者 找了所有以index1为起始点的边没有找到这条边return false;} else if (count == 1) { //如果count=1 说明循环了一次就找到了这条边,这是第一条边//就把以index1为起始点的第一条边指向这条边的下一个,把这条边以index1为起始点的关系解除G.vexlist[index1].firstout = firstOutCur->tlink;} else {//把这条边的上一条边的相同起始点的边 指向 这条边下一条相同起始点的边,把这条边以index1为起始点的关系解除firstOutPre->tlink = firstOutCur->tlink;}targetArc = firstOutCur; //只要没有返回false,证明当前存在这条边//下面的是找以index2为终止点的边 与上面大概类似!!!count = 0; //count重置为0ArcNode *firstInCur = G.vexlist[index2].firstin;ArcNode *firstInPre;while (firstInCur) { //如果以index2为终止点的边不为空,一直循环count++; //每次循环,都是一条新边, count+1if (firstInCur==targetArc) { //如果当前边是上面找出来的那条边,终止循环break;}firstInPre = firstInCur; //当前边保存到pre,当前边继续找index2为终止点的边firstInCur = firstInCur->hlink;}if (count == 0 || !firstOutCur) {cout << "不存在该边" << endl;return false;} else if (count == 1) {G.vexlist[index2].firstin = firstInCur->hlink;} else {firstInPre->hlink = firstInCur->hlink;}G.arcnum--; //删除后图的边数-1cout << vex1 << "->" << vex2 << " 删除成功" << endl;return true;
}//根据下标删除边(删除结点时使用) //删除结点的时候使用此方法,因为要频繁的删除与结点相关的边
bool deleteArc(ALGraph &G, int index1, int index2) { //方法和上面删除边的方法基本类似,这里的下标是不需要输入的ArcNode *firstOutCur = G.vexlist[index1].firstout;ArcNode *firstOutPre;int count = 0;while (firstOutCur) {count++;if (firstOutCur->tailvex == index1 && firstOutCur->headvex == index2) {break;}firstOutPre = firstOutCur;firstOutCur = firstOutCur->tlink;}if (count == 0 || !firstOutCur) {return false;} else if (count == 1) {G.vexlist[index1].firstout = firstOutCur->tlink;} else {firstOutPre->tlink = firstOutCur->tlink;}count = 0;ArcNode *firstInCur = G.vexlist[index2].firstin;ArcNode *firstInPre;while (firstInCur) {count++; //这里可以用下标匹配删除,如果存在多条起点和终点相同的边(平行边),删除的一定是相同一条边!!!//插入边的时候采用的是头插法,最后插入的边一定在最后,// 搜起始点相同的也是先搜到的最后一个边,终止点相同的也是最后一个边if (firstInCur->tailvex == index1 && firstInCur->headvex == index2) {break;}firstInPre = firstInCur;firstInCur = firstInCur->hlink;}if (count == 0 || !firstOutCur) {return false;} else if (count == 1) {G.vexlist[index2].firstin = firstInCur->hlink;} else {firstInPre->hlink = firstInCur->hlink;}G.arcnum--;return true;
}//删除结点
bool deleteVex(ALGraph &G) {cout << "请输入删除的顶点" << endl;int vex, index;cin >> vex;index = getGraphIndex(G, vex);for (int i = 0; i < G.vexnum; ++i) { //循环每一个顶点,删除与他相关的边while (deleteArc(G, index, i));//删除下标 index->i 的边,// 如果删除成功返回true,继续循环,防止有平行边,当删除失败说明不存在边,返回falsewhile(deleteArc(G, i, index)); //同上 删除 i->index 的边}G.vexlist[index].data = -1; //删除完结点,设置此结点的值为-1,表示结点已删除cout << "结点已删除" << endl;
}//添加结点
bool createVex(ALGraph &G) {cout << "请输入添加结点的值" << endl;int data;cin >> data;G.vexlist[G.vexnum].data = data; //设置结点的数值,以该结点为终止点,以该结点为初始点的边赋值空G.vexlist[G.vexnum].firstin = NULL;G.vexlist[G.vexnum].firstout = NULL;G.vexnum++;cout << "添加结点成功" << endl;
}//创建十字链表
bool createGraph(ALGraph &G) {G.vexnum = 0; //图的初始结点数量为0cout << "请输入顶点数量" << endl;int count;cin >> count; //输出顶点数量和边数量for (int i = 0; i < count; i++) { //循环创建count个结点createVex(G);}cout << "请输入边的数量" << endl;cin >> G.arcnum;int v1, v2;for (int i = 0; i < G.arcnum; i++) { //循环创建边createArc(G);}cout << "初始化十字链表成功" << endl;return true;
}//打印十字链表
void printGraph(ALGraph G) {cout <<endl;for (int i = 0; i < G.vexnum; i++) {if (G.vexlist[i].data == -1) { //如果该结点的值为 -1 说明该结点被删除了,跳过本次循环continue;}ArcNode *tail = G.vexlist[i].firstout; //找到第一条以该结点为初始点的边ArcNode *head = G.vexlist[i].firstin; //找到第一条以该结点为终止点的边cout << G.vexlist[i].data << " 起始的边有: ";while (tail) { //输出完当前边的信息,接着找上一条以当前点为初始点的边cout << G.vexlist[tail->tailvex].data << "->" << G.vexlist[tail->headvex].data << " ";tail = tail->tlink;}cout << endl << G.vexlist[i].data << " 结束的边有: ";while (head) { //输出完当前边的信息,接着找上一条以当前点为终止点的边cout << G.vexlist[head->tailvex].data << "->" << G.vexlist[head->headvex].data << " ";head = head->hlink;}cout << endl;}cout << endl;
}int main() {ALGraph G;//输入样例:4 3 1 2 3 4 1 2 1 3 2 3createGraph(G);printGraph(G);int selected;while (true) {cout << "输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出" << endl;cin >> selected;if (selected == 1) {createArc(G);} else if (selected == 2) {deleteArc(G);} else if (selected == 3) {createVex(G);} else if (selected == 4) {deleteVex(G);} else {break;}printGraph(G);}
}输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
请输入顶点数量
4
请输入添加结点的值
0
添加结点成功
请输入添加结点的值
1
添加结点成功
请输入添加结点的值
2
添加结点成功
请输入添加结点的值
3
添加结点成功
请输入边的数量
7
输入边的起始点和终止点
0 1
0->1 创建成功
输入边的起始点和终止点
0 2
0->2 创建成功
输入边的起始点和终止点
2 0
2->0 创建成功
输入边的起始点和终止点
2 3
2->3 创建成功
输入边的起始点和终止点
3 0
3->0 创建成功
输入边的起始点和终止点
3 1
3->1 创建成功
输入边的起始点和终止点
3 2
3->2 创建成功
初始化十字链表成功0 起始的边有: 0->2 0->1
0 结束的边有: 3->0 2->0
1 起始的边有:
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 3->2 0->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 2->3 输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
1
输入边的起始点和终止点
1 2
1->2 创建成功0 起始的边有: 0->2 0->1
0 结束的边有: 3->0 2->0
1 起始的边有: 1->2
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 1->2 3->2 0->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 2->3 输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
2
输入边的起始点和终止点
0 2
0->2 删除成功0 起始的边有: 0->1
0 结束的边有: 3->0 2->0
1 起始的边有: 1->2
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 1->2 3->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 2->3 输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
3
请输入添加结点的值
4
添加结点成功0 起始的边有: 0->1
0 结束的边有: 3->0 2->0
1 起始的边有: 1->2
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 1->2 3->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 2->3
4 起始的边有:
4 结束的边有: 输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
1
输入边的起始点和终止点
1 4
1->4 创建成功0 起始的边有: 0->1
0 结束的边有: 3->0 2->0
1 起始的边有: 1->4 1->2
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 1->2 3->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 2->3
4 起始的边有:
4 结束的边有: 1->4 输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
1
输入边的起始点和终止点
4 3
4->3 创建成功0 起始的边有: 0->1
0 结束的边有: 3->0 2->0
1 起始的边有: 1->4 1->2
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 1->2 3->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 4->3 2->3
4 起始的边有: 4->3
4 结束的边有: 1->4 输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
4
请输入删除的顶点
4
结点已删除0 起始的边有: 0->1
0 结束的边有: 3->0 2->0
1 起始的边有: 1->2
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 1->2 3->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 2->3 输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
qProcess finished with exit code 02.4、邻接多重表
邻接多重表特点:
虽然邻接表已经能很好的表示无向图了,但是如果需要删除一条边<i, j>,则需要去 i,j 中分别删除相邻的结点
邻接多重表,每条边有个边结构体,删除时只需要删除一个边即可,但是要解除这个边的所有关系
邻接多重表中,边与边之间的联系相对密切,很容易找到与某个结点相关的边
邻接多重表结构:
顶点表结点:
mark:哨兵,用来标记当前边是否被访问过。
ivex:当前边相关联的一个结点。
ilink:指向上一条存在 ivex 结点的边。
jvex:当前边相关联的另一个结点。
jlink:指向上一条存在 jvex 结点的边。
info:表示顶点的值
在本篇博客中,做了ivex < jvex 的处理,
不做处理也可以实现,删除边时,相对于本篇博客的代码可能要做一些逻辑修改
邻接多重表例图:

以 <2, 3> 这条边为例子:
可以通过 <2, 1> 这条边的 ilink 找到 <2, 3>
V4 (下标为3) 头结点的第一条相关边为 <2, 3>
可以通过 <2, 3> 这条边的 ilink 找到 <2, 4>
可以通过 <2, 3> 这条边的 jlink 找到 <0, 3>
边与边之间的联系相对密切,很容易找到与某个结点相关的边
邻接多重表示例代码
代码:
#include "iostream"#define MAXSize 100
using namespace std;
typedef struct ArcNode { //边结构体:bool visited; //记录此边是否被访问int ivex, jvex; //记录此边的两个结点 i j(这里存放的是两个结点的下标)// (笔者边结点保证了,下标小的为i,下标大的为j,如果不做处理,后面删除边也要修改逻辑)struct ArcNode *ilink, *jlink; //ilink指向上一条和当前边 ivex 相同的边(上一条边的ivex 或者 jvex 和当前边的ivex相等)// ,jlink也是指向上一条和 jvex 相关的边int info; //用来记录这条边的权重
} ArcNode;
typedef struct VexNode { //结点结构体: 结点的值,firstedge指向与结点相关的第一条边int data;ArcNode *firstedge;
} VexNode;
typedef struct { //图结构体:结点的数组(表头为结点,结点后面跟指针),vexnum 结点的数量,arcnum 边结点的数量VexNode adjmulist[MAXSize];int vexnum, arcnum;
} AMLGraph;//找到顶点在表头结点的下标
int getGraphIndex(AMLGraph G, int targetnode) { //通过结点的值,找到在图中表头结点的下标(如果不存在,返回-1)for (int i = 0; i < G.vexnum; i++) {if (G.adjmulist[i].data == targetnode) {return i;}}return -1;
}//创建边
bool createArc(AMLGraph &G) {int vex1, vex2, index1, index2;cout << "请输入新建边的两个结点" << endl;cin >> vex1 >> vex2;index1 = getGraphIndex(G, vex1); //找到两个结点在结点数组中的下标index2 = getGraphIndex(G, vex2);ArcNode *newedge = new ArcNode; //构建一个新边ArcNode *oldfirstegde; //!!!if (index1 > index2) { //保证index1 <= index2 这么做是为了里面边的 i j 相对有序(如果不保证有序,但是后面删除边的逻辑要记得修改)index1 ^= index2;index2 ^= index1;index1 ^= index2;}newedge->ivex = index1; //新边为i j 之间的边,边的两个结点要赋值i jnewedge->jvex = index2;//把新边连接到下标index1 和 index2 两个头结点的第一条边//相当于链表插入,头插法oldfirstegde = G.adjmulist[index1].firstedge; //找到当前index1下标的结点的第一条边G.adjmulist[index1].firstedge = newedge; //把新边绑定到index1的第一条边newedge->ilink = oldfirstegde; //新边的ivex 和index1相等的,把老边绑定到新边的ilink//与上面类似,是插入到index2头结点的第一条边oldfirstegde = G.adjmulist[index2].firstedge;G.adjmulist[index2].firstedge = newedge;newedge->jlink = oldfirstegde;G.arcnum++;return true;
}//通过下标找到边,在表头结点target相关的边 中 解除这条边的关系 //(target是index1 或者index2的其中一个)
bool deleteArc(AMLGraph &G, int index1, int index2, int target) { //找到一条下标index1 和 index2相关的边,删除下标 target 中此边的关系ArcNode *curArc = G.adjmulist[target].firstedge; //找到target下标结点的第一条边ArcNode *preArc; //记录当前边的上一条边,如果cur是要删除的边,直接pre下一条的关系连接到cur下一条的关系int count = 0;while (curArc) { //此边不为空,一直循环count++; //每次循环一条边,count+1,,记录目标边是第几条if (curArc->ivex == index1 && curArc->jvex == index2) { //如果找到此边,退出循环break;}preArc = curArc; //当前边给pre,cur继续去找下一条边//这里通过ivex 或者 jvex 找到下一条有关系的点//如果 ivex 是 index1 或者 index2 ,就找ivex相关的下一条边,指向->ilinkif (curArc->ivex == index1 || curArc->ivex == index2) { //如果ivex结点为index1或者index2其中的一个curArc = curArc->ilink;//其他情况下就是 jvex 是 index1 或者 index2,就找jlink} else {curArc = curArc->jlink;}}if (count == 0 || !curArc) { //如果没有循环,或者cur指向空结点了,说明没有此边
// cout << "当前边不存在" << endl;return false;} else if (count == 1) { //如果只循环了一次,说明是表头结点的第一条相关的边if (curArc->ivex == target) { //如果是 ivex 结点与target相关 就把当前边的 ilink 赋值给表头结点的第一条边G.adjmulist[target].firstedge = curArc->ilink;} else { //否则就是 jvex 结点与target相关,把当前边的jlink给表头结点的第一条边G.adjmulist[target].firstedge = curArc->jlink;}} else { //如果pre的ivex 和 cur的ivex 相等,说明两个边都是通过 ilink 连接的,cur->ilink和pre->ilink是同一个ivex相关联的点// 删除当前边的关系,把cur->ilink 赋值给pre->ilink//这里举个例子:头结点下标为 0 的边 <0,1>,<0,2>,<0,3> cur指向<0,2> pre指向<0,1>//两个边是通过 ivex 相连的,直接把pre->ilink 指向 cur->ilink (下面的大家可以自己举个例子理解理解)if (preArc->ivex == curArc->ivex) {preArc->ilink = curArc->ilink;//pre->ivex和cur->jvex相关联 例子:头结点下标为 5 的边 <5,6>,<3,5>,<5,7>} else if (preArc->ivex == curArc->jvex) {preArc->ilink = curArc->jlink;//例子:头结点下标为 5 的边 <0,5>,<5,7>,<3,5>} else if (preArc->jvex == curArc->ivex) {preArc->jlink = curArc->ilink;//例子:头结点下标为 5 的边 <0,5>,<3,5>,<5,7>} else if (preArc->jvex == curArc->jvex) {preArc->jlink = curArc->jlink;}//一共就是这四种关系,大家可以多对应图,理解理解}return true;
}//删除边
bool deleteArc(AMLGraph &G) {int vex1, vex2, index1, index2;cout << "请输入删除边的两个结点" << endl;cin >> vex1 >> vex2;index1 = getGraphIndex(G, vex1);index2 = getGraphIndex(G, vex2);if (index1 > index2) { //保证index1 <= index2 这么做是为了里面边的 i j 相对有序(如果没有这一步后面可能删除边会相对麻烦一些)index1 ^= index2;index2 ^= index1;index1 ^= index2;}//删除index1 和 index2 相对于 index1 和 index2 头结点的关系if (deleteArc(G, index1, index2, index1) && deleteArc(G, index1, index2, index2)) {cout << vex1 << "->" << vex2 << "边删除成功" << endl;return true;} else {cout << vex1 << "->" << vex2 << "边删除失败" << endl;return false;}
}//创建结点
bool createVex(AMLGraph &G) {cout << "请输入要创建的结点的值" << endl;int data;cin >> data;G.adjmulist[G.vexnum].data = data; //给结点赋值,结点的第一条有关的边设为空,图中结点数量+1G.adjmulist[G.vexnum].firstedge = NULL;G.vexnum++;return true;
}//删除结点
bool deleteVex(AMLGraph &G) {cout << "请输入要删除的结点" << endl;int vex;cin >> vex;int index = getGraphIndex(G, vex); //找到要删除结点的下标for (int i = 0; i < G.vexnum; i++) { //循环每个结点,删除所有结点与目标结点的关系while (deleteArc(G, i, index, i)); //这里用while,是防止存在多条边的情况(当要删除的边不存在的时候会返回false)while (deleteArc(G, i, index, index)); // 解除表头结点 i 中这条边的关系}G.adjmulist[index].data = -1; //结点删除后,把当前结点的值标记为 -1 ,表明该点已被删除return true;
}//初始化创建图
bool createAMLGraph(AMLGraph &G) {cout << "请输入结点数" << endl;int vexCount;cin >> vexCount;G.vexnum = 0; //初始化时,G的顶点数量为0for (int i = 0; i < vexCount; ++i) {createVex(G);}cout << "请输入边数" << endl;int arcCount;cin >> arcCount;for (int i = 0; i < arcCount; ++i) {createArc(G);}cout << "邻接多重表初始化完成" << endl;return true;
}//输出邻接多重表
bool printAMLGraph(AMLGraph G) {for (int i = 0; i < G.vexnum; i++) { //循环图中的每一个点if (G.adjmulist[i].data == -1) { //如果当前点的值为 -1 ,说明当前点已被删除continue;}cout << G.adjmulist[i].data;ArcNode *demo = G.adjmulist[i].firstedge;while (demo) { //找到当前表头结点的第一个边,cout << " " << demo->ivex << "<->" << demo->jvex; //输出当前边的两个结点demo = demo->ivex == i ? demo->ilink : demo->jlink; //如果当前点的ivex与表头结点相关,就指向ilink,否则就是jvex与表头结点相关}cout << endl;}return true;
}int main() {AMLGraph G;createAMLGraph(G); //初始化图printAMLGraph(G);int selected;while (true) {cout << "输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出" << endl;cin >> selected;if (selected == 1) {createArc(G); //创建边} else if (selected == 2) {deleteArc(G); //删除边} else if (selected == 3) {createVex(G); //创建结点} else if (selected == 4) {deleteVex(G); //删除结点} else {break;}printAMLGraph(G); //每次都输出图}return 0;
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
请输入结点数
4
请输入要创建的结点的值
0
请输入要创建的结点的值
1
请输入要创建的结点的值
2
请输入要创建的结点的值
3
请输入边数
5
请输入新建边的两个结点
0 1
请输入新建边的两个结点
0 2
请输入新建边的两个结点
0 3
请输入新建边的两个结点
1 3
请输入新建边的两个结点
2 3
邻接多重表初始化完成
0 0<->3 0<->2 0<->1
1 1<->3 0<->1
2 2<->3 0<->2
3 2<->3 1<->3 0<->3
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
1
请输入新建边的两个结点
1 2
0 0<->3 0<->2 0<->1
1 1<->2 1<->3 0<->1
2 1<->2 2<->3 0<->2
3 2<->3 1<->3 0<->3
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
2
请输入删除边的两个结点
0 3
0->3边删除成功
0 0<->2 0<->1
1 1<->2 1<->3 0<->1
2 1<->2 2<->3 0<->2
3 2<->3 1<->3
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
3
请输入要创建的结点的值
4
0 0<->2 0<->1
1 1<->2 1<->3 0<->1
2 1<->2 2<->3 0<->2
3 2<->3 1<->3
4
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
1
请输入新建边的两个结点
1 4
0 0<->2 0<->1
1 1<->4 1<->2 1<->3 0<->1
2 1<->2 2<->3 0<->2
3 2<->3 1<->3
4 1<->4
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
4
请输入要删除的结点
4
0 0<->2 0<->1
1 1<->2 1<->3 0<->1
2 1<->2 2<->3 0<->2
3 2<->3 1<->3
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
qProcess finished with exit code 0三、图的遍历
3.1、深度优先搜索
深度优先搜索概念:
深度优先搜索: 是沿着一个方向访问到底,访问过的点,进行标记,然后在从底换一个方向继续访问,访问下一个点的时候,如果被 标记过就不在访问。直到所有的点都被标记了,说明每个点都被访问了。
其实有点类似树的递归遍历(先,中,后序遍历),先向左下方向找到底,然后在返回上一个结点的右子树接着找, 找完继续返回上个结点,换个方向继续找,不断这么重复递归,即可完成所有结点的遍历
总之,记住一句话,深度优先查找就是先尽可能达到当前遍历路径能够达到最长的路径,一旦达到该路径终点,再回 溯,从原来已遍历过顶点(PS:该顶点包含多个分支路径)处开始新的分支路径遍历。
深度优先搜索例图:

深度优先搜索的方向顺序,起点可以自己选择
这里我们先从左下方向搜,然后再向右下方向走,然后右上,左上
例如:从 V1 开始 访问 V1,V1 标记已访问
V1 -> V2 V2 标记已访问,继续向这个方向搜索下一个
V2 -> V4 V4 标记已访问,继续向这个方向搜索
V4 -> V8 V4 左下方向已经没有结点了,找右下方向 V8 ,V8标记访问
V8 -> V5 V8 下方没有结点了,找左上 V5 ,V5标记访问
V1 -> V3 V5相连的没有未访问的结点了,只能返回V5->V8->V4->V2->V1 ,V1 以前的结点都被访问了,访问V3,标记V3已访问
V3 -> V6 V6 标记已访问,继续向这个方向搜索
V6 -> V7 V6 左下方向已经没有结点了,找右下方向 V7 ,V7标记访问
V7 没有未访问结点了,返回 V7->V6->V3->V1 全部访问了,图遍历完成V1 -> V2 -> V4 -> V8 -> V5 -> V3 -> V6 -> V7
深度优先搜索示例代码(邻接矩阵存储图):
此处借用算法设计与分析基础(第三版)上一段概念介绍,及说明图形介绍其具体遍历过程,下面的具体代码使用数据就是下图中相关数据。


代码:
#include "iostream"using namespace std;int count = 0; //用于计算遍历总次数
int value[10]; //初始化后,各元素均为0
char result[10];/*
* adjMatrix是待遍历图的邻接矩阵
* value是待遍历图顶点用于是否被遍历的判断依据,0代表未遍历,非0代表已被遍历
* result用于存放深度优先遍历的顶点顺序
* number是当前正在遍历的顶点在邻接矩阵中的数组下标编号
*/
void dfsVisit(int adjMatrix[10][10], int number) {value[number] = ++count; //把++count赋值给当前正在遍历顶点判断值数组元素,变为非0,代表已被遍历cout << "当前已行走顶点value[" << number << "] = " << value[number] << " ";for (int i = 0; i < 10; i++) {if (adjMatrix[number][i] == 1 && value[i] == 0) { //当当前顶点的相邻有相邻顶点可行走且其为被遍历char temp = (char) ('a' + i);result[count] = temp; //存放即将行走的顶点下标字母cout << " 当前i值:" << i << " 到达" << temp << "地" << endl;dfsVisit(adjMatrix, i); //执行递归,行走第i个顶点}}
}/** adjMatrix是待遍历图的邻接矩阵* value是待遍历图顶点用于是否被遍历的判断依据,0代表未遍历,非0代表已被遍历* result用于存放深度优先遍历的顶点顺序*/
void dfs(int adjMatrix[10][10] ) {for (int i = 0; i < 10; i++) {if (value[i] == 0) {char temp = (char) ('a' + i);cout << "深度为:" << i << ",当前出发点:" << temp << endl;result[i] = temp; //存放当前正在遍历顶点下标字母dfsVisit(adjMatrix, i);}}
}int main() {int adjMatrix[10][10] = {{0, 0, 1, 1, 1, 0, 0, 0, 0, 0},{0, 0, 0, 0, 1, 1, 0, 0, 0, 0},{1, 0, 0, 1, 0, 1, 0, 0, 0, 0},{1, 0, 1, 0, 0, 0, 0, 0, 0, 0},{1, 1, 0, 0, 0, 1, 0, 0, 0, 0},{0, 1, 1, 0, 1, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 1, 0, 1},{0, 0, 0, 0, 0, 0, 1, 0, 1, 0},{0, 0, 0, 0, 0, 0, 0, 1, 0, 1},{0, 0, 0, 0, 0, 0, 1, 0, 1, 0}};dfs(adjMatrix);cout << endl << "深度优先查找遍历顺序如下:" << endl;for (int i = 0; i < 10; i++)cout << " " << result[i];return 0;
}输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
深度为:0,当前出发点:a
当前已行走顶点value[0] = 1 当前i值:2 到达c地
当前已行走顶点value[2] = 2 当前i值:3 到达d地
当前已行走顶点value[3] = 3 当前i值:5 到达f地
当前已行走顶点value[5] = 4 当前i值:1 到达b地
当前已行走顶点value[1] = 5 当前i值:4 到达e地
当前已行走顶点value[4] = 6 深度为:6,当前出发点:g
当前已行走顶点value[6] = 7 当前i值:7 到达h地
当前已行走顶点value[7] = 8 当前i值:8 到达i地
当前已行走顶点value[8] = 9 当前i值:9 到达j地
当前已行走顶点value[9] = 10
深度优先查找遍历顺序如下:a c d f b e g h i j
Process finished with exit code 03.2、广度优先搜索
广度优先搜索概念:
广度优先查找(Breadth-first Search,BFS)按照一种同心圆的方式,首先访问所有和初始顶点邻接的顶点,然后是离它两条边的所有未访问顶点,以此类推,直到所有与初始顶点同在一个连通分量中的顶点都被访问过了为止。如果仍然存在未被访问的顶点,该算法必须从图的其他连接分量中的任意顶点重新开始。
广度优先搜索例图:
百度百科:
1代表第一步要走的点,2代表第二步要走的点……

广度优先搜索示例代码(邻接矩阵存储图):
此处借用《算法设计与分析基础》(第3版)上一段文字介绍及其配图来讲解,下面程序中使用的图就是配图中所给的数据,在程序中,使用邻接矩阵来表示配图中图。


PS:下面所给程序的运行结果和配图中图(b)顺序在fb那两个位置不一致,下面程序运行结果顺序是a c d e b f g h j i,原因是在遍历的过程中,我所写代码是按照字母顺序来进行遍历的,书上所讲可能是使用链表来存储顶点,具体怎么实现本人也未去仔细探讨…
代码:
#include "iostream"using namespace std;int count = 0; //用于计算遍历总次数
int value[10]; //初始化后,各元素均为0
char result[10];/*
* adjMatrix是待遍历图的邻接矩阵
* value是待遍历图顶点用于是否被遍历的判断依据,0代表未遍历,非0代表已被遍历,其最终具体结果代表该顶点在最终遍历顺序中的位置
* result用于存放广度优先遍历的顶点顺序
* number是当前正在遍历的顶点在邻接矩阵中的数组下标编号
*/
void bfsVisit(int adjMatrix[10][10] ,int number){value[number] = ++count; //出发顶点已被遍历,其在遍历结果中最终位置为++countfor(int i = 0;i < 10;i++){if(adjMatrix[number][i] == 1 && value[i] == 0){ //当改顶点与出发顶点相邻且未被遍历时char temp = (char) ('a' + i);result[count] = temp;cout << endl;cout << "到达" << temp << "地" << "\t";value[i] = ++count; //当前被遍历顶点,其在遍历结果中最终位置为++count}}
}/** adjMatrix是待遍历图的邻接矩阵* value是待遍历图顶点用于是否被遍历的判断依据,0代表未遍历,非0代表已被遍历,其最终具体结果代表该顶点在最终遍历顺序中的位置* result用于存放广度优先遍历的顶点顺序*/void bfs(int adjMatrix[10][10]){for(int i = 0;i < 10;i++){if(value[i] == 0){ //当该顶点未被遍历时char temp = (char) ('a' + i);result[count] = temp;cout << endl << "出发点:" << temp << "地";bfsVisit(adjMatrix,i); //使用迭代遍历该顶点周边所有邻接顶点}}
}int main() {int adjMatrix[10][10] = {{0, 0, 1, 1, 1, 0, 0, 0, 0, 0},{0, 0, 0, 0, 1, 1, 0, 0, 0, 0},{1, 0, 0, 1, 0, 1, 0, 0, 0, 0},{1, 0, 1, 0, 0, 0, 0, 0, 0, 0},{1, 1, 0, 0, 0, 1, 0, 0, 0, 0},{0, 1, 1, 0, 1, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 1, 0, 1},{0, 0, 0, 0, 0, 0, 1, 0, 1, 0},{0, 0, 0, 0, 0, 0, 0, 1, 0, 1},{0, 0, 0, 0, 0, 0, 1, 0, 1, 0}};bfs(adjMatrix);cout << endl << "广度优先查找遍历顺序如下:" << endl;for (int i = 0; i < 10; i++)cout << " " << result[i];return 0;
}输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph出发点:a地
到达c地
到达d地
到达e地
出发点:b地
到达f地
出发点:g地
到达h地
到达j地
出发点:i地
广度优先查找遍历顺序如下:a c d e b f g h j i
Process finished with exit code 03.3、Dijkstra最短路径
Dijkstra概念:
Dijkstra算法功能:给出加权连通图中一个顶点,称之为起点,找出起点到其它所有顶点之间的最短距离。
Dijkstra算法思想:采用贪心法思想,进行n-1次查找(PS:n为加权连通图的顶点总个数,除去起点,则剩下n-1个顶点),第一次进行查找,找出距离起点最近的一个顶点,标记为已遍历;下一次进行查找时,从未被遍历中的顶点寻找距离起点最近的一个顶点, 标记为已遍历;直到n-1次查找完毕,结束查找,返回最终结果。
Dijkstra例图:
使用Dijkstra算法得到最短距离示例
此处借用文末参考资料1博客中一个插图(PS:个人感觉此图描述简单易懂):


Dijkstra示例代码(邻接矩阵存储图):
Dijkstra复杂度是O(N^2),如果用binary heap优化可以达到O((E+N)logN),用fibonacci heap可以优化到O(NlogN+E) 。
注意,Dijkstra算法只能应用于不含负权值的图。因为在大多数应用中这个条件都满足,所以这种局限性并没有影响Dijkstra算法的广泛应用。
其次,大家要注意把Dijkstra算法与寻找最小生成树的Prim算法区分开来。两者都是运行贪心法思想,但是Dijkstra算法是比较路径的长度,所以必须把起点到相应顶点之间的边的权重相加,而Prim算法则是直接比较相应边给定的权重。
下面的代码时间复杂度为O(N^2),代码中所用图为2.1使用Dijkstra算法得到最短距离示例中所给的图。
代码:
#include "iostream"using namespace std;/** 参数adjMatrix:为图的权重矩阵,权值为-1的两个顶点表示不能直接相连* 函数功能:返回顶点0到其它所有顶点的最短距离,其中顶点0到顶点0的最短距离为0*/int result[6]; //用于存放顶点0到其它顶点的最短距离void getShortestPaths(int adjMatrix[6][6]) {bool used [6] ; //用于判断顶点是否被遍历used[0] = true; //表示顶点0已被遍历for(int i = 1;i < 6;i++) {result[i] = adjMatrix[0][i];used[i] = false;}for(int i = 1;i < 6;i++) {int min = 0xffff; //用于暂时存放顶点0到i的最短距离,初始化为Integer型最大值int k = 0;for(int j = 1;j < 6;j++) { //找到顶点0到其它顶点中距离最小的一个顶点if(!used[j] && result[j] != -1 && min > result[j]) {min = result[j];k = j;}}used[k] = true; //将距离最小的顶点,记为已遍历for(int j = 1;j < 6;j++) { //然后,将顶点0到其它顶点的距离与加入中间顶点k之后的距离进行比较,更新最短距离if(!used[j]) { //当顶点j未被遍历时//首先,顶点k到顶点j要能通行;这时,当顶点0到顶点j的距离大于顶点0到k再到j的距离或者顶点0无法直接到达顶点j时,更新顶点0到顶点j的最短距离if(adjMatrix[k][j] != -1 && (result[j] > min + adjMatrix[k][j] || result[j] == -1))result[j] = min + adjMatrix[k][j];}}}
}int main() {int adjMatrix[6][6] = {{0,6,3,-1,-1,-1},{6,0,2,5,-1,-1},{3,2,0,3,4,-1},{-1,5,3,0,2,3},{-1,-1,4,2,0,5},{-1,-1,-1,3,5,0}};getShortestPaths(adjMatrix);cout << "顶点0到图中所有顶点之间的最短距离为:" << endl;for(int i = 0;i < 6;i++)cout << result[i] << " ";
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
顶点0到图中所有顶点之间的最短距离为:
0 5 3 6 7 9
Process finished with exit code 0
3.4、Floyd最短路径
Floyd概念:
Floyd算法功能:给定一个加权连通图,求取从每一个顶点到其它所有顶点之间的最短距离。(PS:其实现功能也称完全最短路径问题)
Floyd算法思想:将顶点i到j的直接距离依次与顶点i到顶点j之间加入k个中间节点之后的距离进行比较,从中选出最短的一组距离,即为顶点i到顶点j的最短距离,然后重复上述步骤求取其它顶点之间的最短距离。
Floyd例图:
使用Floyd算法得到最短距离示例**
此处借用《算法设计与分析基础》第3版上一个插图:
其中,
D(0)表示不包含中间节点,即给定图的原始权重矩阵;
D(1)表示加入一个中间节点a;
D(2)表示在D(1)的基础上再加入一个中间节点b;
D(3)表示在D(2)的基础上再加入一个中间节点c;
D(4)表示在D(3)的基础上再加入一个中间节点d,这时就可得到最终结果。
每次加入一个中间节点后,都要更新所有顶点之间的最短距离,
直到所有顶点均可以作为中间顶点之后,才算更新完毕,即可得到最终结果。

Floyd示例代码(邻接矩阵存储图):
Floyd是计算每对顶点间最短路径的经典算法,其采用的思想是动态规划法。
时间复杂度是雷打不动的O(n^3)。
注意,Floyd算法计算最短距离可以有负权值的边,但不能有权值和为负数的回路。
下面代码中所用图的数据便是2.1中示例图的数据。
代码:
#include "iostream"using namespace std;/** 参数adjMatrix:给定连通图的权重矩阵,其中权重为-1表示两个顶点不能直接相连* 函数功能:返回所有顶点之间的最短距离权重矩阵*/
void getShortestPaths(int adjMatrix[4][4]) {for (int k = 0; k < 4; k++) {for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++) {if (adjMatrix[i][k] != -1 && adjMatrix[k][j] != -1) {int temp = adjMatrix[i][k] + adjMatrix[k][j]; //含有中间节点k的顶点i到顶点j的距离if (adjMatrix[i][j] == -1 || adjMatrix[i][j] > temp)adjMatrix[i][j] = temp;}}}}
}int main() {int adjMatrix[4][4] = {{0, -1, 3, -1},{2, 0, -1, -1},{-1, 7, 0, 1},{6, -1, -1, 0}};getShortestPaths(adjMatrix);cout << "使用Floyd算法得到的所有顶点之间的最短距离权重矩阵为:" << endl;for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++) {cout << adjMatrix[i][j] << " ";}cout << endl;}return 0;
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
使用Floyd算法得到的所有顶点之间的最短距离权重矩阵为:
0 10 3 4
2 0 5 6
7 7 0 1
6 16 9 0 Process finished with exit code 03.5、Prim最短路径
Prim概念:
普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克(英语:Vojtěch Jarník)发现;并在1957年由美国计算机科学家罗伯特·普里姆(英语:Robert C. Prim)独立发现;1959年,艾兹格·迪科斯彻再次发现了该算法。因此,在某些场合,普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆-亚尔尼克算法。
原理简单介绍:
1).输入:一个加权连通图,其中顶点集合为V,边集合为E;
2).初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空;
3).重复下列操作,直到Vnew = V:
a.在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
b.将v加入集合Vnew中,将<u, v>边加入集合Enew中;
4).输出:使用集合Vnew和Enew来描述所得到的最小生成树。
Prim例图:
本文具体编码使用数据参考自《算法设计与分析基础》第三版,下面是其具体图示:



Prim示例代码(邻接矩阵存储图):
代码:
#include "iostream"
#include "vector"using namespace std;/** 参数G:给定的图,其顶点分别为0~G.length-1,相应权值为具体元素的值* 函数功能:返回构造生成的最小生成树,以二维数组形式表示,其中元素为0表示最小生成树的边*/
void getMinTree(int G[6][6]) {int result[6][6] = {{-1, 3, -1, -1, 6, 5},{3, -1, 1, -1, -1, 4},{-1, 1, -1, 6, -1, 4},{-1, -1, 6, -1, 8, 5},{6, -1, -1, 8, -1, 2},{5, 4, 4, 5, 2, -1}};int vertix[6]; //记录顶点是否被访问,如果已被访问,则置相应顶点的元素值为-2for (int i = 0; i < 6; i++)vertix[i] = i;vector<int> listV; //保存已经遍历过的顶点listV.push_back(0); //初始随意选择一个顶点作为起始点,此处选择顶点0vertix[0] = -2; //表示顶点0被访问while (listV.size() < 6) { //当已被遍历的顶点数等于给定顶点数时,退出循环int minDistance = 0xffff; //用于寻找最小权值,初始化为int最大值,相当于无穷大的意思int minV = -1; //用于存放未被遍历的顶点中与已被遍历顶点有最小权值的顶点int minI = -1; //用于存放已被遍历的顶点与未被遍历顶点有最小权值的顶点 ;即G[minI][minV]在剩余的权值中最小for (int i = 0; i < listV.size(); i++) { //i 表示已被访问的顶点int v1 = listV[i];for (int j = 0; j < 6; j++) {if (vertix[j] != -2) { //满足此条件的表示,顶点j未被访问if (G[v1][j] != -1 && G[v1][j] < minDistance) {//G[v1][j]值为-1表示v1和j是非相邻顶点minDistance = G[v1][j];minV = j;minI = v1;}}}}vertix[minV] = -2;listV.push_back(minV);result[minI][minV] = 0;result[minV][minI] = 0;}cout << "使用Prim算法,对于给定图中的顶点访问顺序为:" << endl; for (int i = 0; i < listV.size(); i++) {cout << listV[i] << " ";}cout << endl;cout << "使用Prim算法,构造的最小生成树的二维数组表示如下(PS:元素为0表示树的边):" << endl;for (int i = 0; i < 6; i++) {for (int j = 0; j < 6; j++)cout << result[i][j] << "\t";cout << endl;}
}int main() {int G[6][6] = {{-1, 3, -1, -1, 6, 5},{3, -1, 1, -1, -1, 4},{-1, 1, -1, 6, -1, 4},{-1, -1, 6, -1, 8, 5},{6, -1, -1, 8, -1, 2},{5, 4, 4, 5, 2, -1}};getMinTree(G);return 0;
}输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
使用Prim算法,对于给定图中的顶点访问顺序为:
0 1 2 5 4 3
使用Prim算法,构造的最小生成树的二维数组表示如下(PS:元素为0表示树的边):
-1 0 -1 -1 6 5
0 -1 0 -1 -1 0
-1 0 -1 6 -1 4
-1 -1 6 -1 8 0
6 -1 -1 8 -1 0
5 0 4 0 0 -1 Process finished with exit code 022计算机408考研—数据结构—图相关推荐
- 计算机队列概念,2020计算机专业考研数据结构知识点:栈、队列和数组
2020计算机专业考研数据结构知识点:栈.队列和数组 1.栈.队列的定义及其相关数据结构的概念,包括:顺序栈.链栈.循环队列.链队列等.栈与队列存取数据(请注意包括:存和取两部分)的特点. 2. 掌握 ...
- 计算机考研408哪个视频好,计算机408考研视频哪个好
计算机408考研视频哪个好?看着这样那样的计算机408考研视频,很多考生都无从下手,不知哪个对自己才有用.找计算机408考研视频还是要看老师,比较牛叉的老师如白龙飞等,都在新东方授课.建议考生们选择之 ...
- 计算机408考试题库百度云,2017年计算机408考研真题.pdf
2017年计算机408考研真题.pdf 2017年全国硕士研究生招生考试 计算机科学与技术学科联考 计算机学科专业基础综合试题 一.单项选择题:1-40小题,每小题2分,共80分.下列每题给出的四个选 ...
- 2017计算机考研408试卷,2017计算机408考研真题
2017计算机408考研真题 2017年全国硕士研究生招生考试年全国硕士研究生招生考试 计算机科学与技术学科联考计算机科学与技术学科联考 计算机学科专业基础综合试题计算机学科专业基础综合试题 一.单项 ...
- 2022计算机考研全改408,2022计算机408考研大纲
2022计算机408考研大纲还未公布,一起来看看2021计算机408考研大纲原文吧~更多浙江院校发布考研大纲时间.考研大纲内容.考研大纲解析等信息请关注四川考研大纲. I 考试性质 计算机学科专业基础 ...
- (王道408考研数据结构)第三章栈和队列-第三节1:栈的应用之括号匹配问题和表达式问题(前缀、中缀和后缀)
前面我们就说过,栈是一种先进后出的线性表,这种先进后出的特性就决定了它在一类场合或问题中会经常被用到--递归.考研数据结构中所涉及的利用栈结构解决递归问题或者考察栈结构特性的问题主要有这么几类 括号匹 ...
- 计算机408知识点大全,2022计算机408考研知识点:输入输出系统
2022计算机408考研知识点:输入输出系统 如果你准备考计算机专业研究生,小编敬佩你的勇气,作为专业难度很高的计算机专业来说,一定要全力备考.本文新东方在线计算机考研小编整理分享"2022 ...
- 计算机408考研究竟有多难?
过来人现身说法,准确的说,计算机408恐怖,但不难. 我不是在劝退,但我想问,你的目标坚定吗?你准备好了面对吗? 1 考试内容多:虽然未见的像很多人说的,计算机专业课难度第一,但是408的四门课,没有 ...
- 计算机专业考研数据结构比较,计算机专业考研科目:数据结构重点汇总
今天说说文都考研网小编为同学们整理了数据结构科目的重点知识点,供大家参考复习. 1.数据结构的基本概念.基本原理和基本方法,能够对算法进行基本的时间复杂度和空间复杂度的分析;能够运用数据结构的基本原理 ...
- 计算机类考研数据结构,【择校必看】十三所计算机专业课只考数据结构的985院校!...
该楼层疑似违规已被系统折叠 隐藏此楼查看此楼 敲黑板: 本文涉及到的学校计算机专业考研只考数据结构,其中部分院校同时也会考算法.C语言等相关内容.但是,相对其他几门,无疑在专业课的复习上大大降低了难度 ...
最新文章
- entjs 键盘监听
- Python之Pandas:利用pandas实现行数据添加,即将字典格式的数据,按照行数据,从头开始循环添加到dataframe中
- 公网传输技术之SRT协议解析(上)
- [NOIP2014]飞扬的小鸟
- 前端学习(535):多列布局2
- log解析工具 px4_console.log(console.log) = ?
- 商户定价模型—风控人又一经典必学知识
- EF框架step by step(1)—Database-First
- 创新不是突然而至——它是慢慢成长的
- inkscape矢量图_使用Inkscape创建矢量图形的教程
- 【每周荐书系列】——《认知盈余》
- addr2line来定位问题
- 「程序猿 DD」星球活动第一期,将在 7 月 9 日晚 20:00 整开放!
- c51单片机音乐门铃C语言程序,89c51六首歌曲的音乐门铃程序
- 计算机专业买哪一款华硕电脑好,华硕笔记本哪款好 如何挑选笔记本电脑
- 移动云平台的基础架构之旅(一):云应用
- android曲面屏点击事件无响应,都说曲面屏中看不中用,主要原因有四点,第三点是关键!...
- 360手机刷机:360N7pro刷机
- 利用IDEA将项目打包(两种方法)
- 【C++FunCode】基于Funcode使用C++语言编写小游戏(小鲨鱼历险记)
