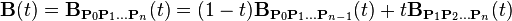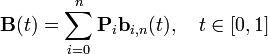Bezier曲线原理

一、原理：

贝塞尔曲线于1962年，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau 于1959年运用de Casteljau 算法开发，以稳定数值的方法求出贝塞尔曲线。

线性贝塞尔曲线

给定点 P₀、P₁，线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出：

且其等同于线性插值。

二次方贝塞尔曲线的路径由给定点 P₀、P₁、P₂ 的函数B(t) 追踪：

。

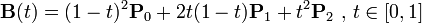TrueType 字型就运用了以贝塞尔样条组成的二次贝塞尔曲线。

P₀、P₁、P₂、P₃ 四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于P₀ 走向 P₁，并从 P₂ 的方向来到P₃。一般不会经过 P₁ 或 P₂；这两个点只是在那里提供方向资讯。P₀ 和 P₁ 之间的间距，决定了曲线在转而趋进 P₃ 之前，走向 P₂ 方向的“长度有多长”。

曲线的参数形式为：

。

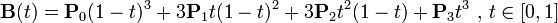现代的成象系统，如 PostScript、Asymptote 和Metafont，运用了以贝塞尔样条组成的三次贝塞尔曲线，用来描绘曲线轮廓。

一般化

P₀、P₁、…、P_n，其贝塞尔曲线即

。

例如：

。

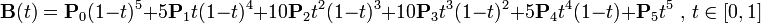如上公式可如下递归表达：用表示由点P₀、P₁、…、P_n 所决定的贝塞尔曲线。则

用平常话来说，阶贝塞尔曲线之间的插值。

一些关于参数曲线的术语，有

即多项式

又称作 n 阶的伯恩斯坦基底多项式，定义 0⁰ = 1。

点 P_i 称作贝塞尔曲线的控制点。多边形以带有线的贝塞尔点连接而成，起始于P₀ 并以 P_n 终止，称作贝塞尔多边形（或控制多边形）。贝塞尔多边形的凸包（convex hull）包含有贝塞尔曲线。

线性贝塞尔曲线函数中的 t 会经过由 P₀ 至P₁ 的B(t) 所描述的曲线。例如当 t=0.25 时，B(t) 即一条由点P₀ 至 P₁ 路径的四分之一处。就像由 0 至 1 的连续t，B(t) 描述一条由 P₀ 至 P₁ 的直线。

为建构二次贝塞尔曲线，可以中介点 Q₀ 和 Q₁ 作为由 0 至 1 的t：

由 P₀ 至 P₁ 的连续点 Q₀，描述一条线性贝塞尔曲线。
由 P₁ 至 P₂ 的连续点 Q₁，描述一条线性贝塞尔曲线。
由 Q₀ 至 Q₁ 的连续点 B(t)，描述一条二次贝塞尔曲线。

为建构高阶曲线，便需要相应更多的中介点。对于三次曲线，可由线性贝塞尔曲线描述的中介点 Q₀、Q₁、Q₂，和由二次曲线描述的点R₀、R₁ 所建构：

对于四次曲线，可由线性贝塞尔曲线描述的中介点 Q₀、Q₁、Q₂、Q₃，由二次贝塞尔曲线描述的点R₀、R₁、R₂，和由三次贝塞尔曲线描述的点S₀、S₁ 所建构：

P(t)=(1-t)P₀+tP₁ ,
矩阵表示为：

P(t)=(1-t)²P₀+2t(1-t)P₁+t²P₂,
矩阵表示为：

P(t)=(1-t)³P₀+3t(1-t)²P₁+3t²(1-t)P₂+t³P₃
矩阵表示为：

在（6－3－2）式中，Mⁿ⁺¹是一个n＋1阶矩阵，称为n次Bezier矩阵。

其中，

利用（6－3－3）式，我们可以得到任意次Bezier矩阵的显式表示，例如4次和5次Bezier矩阵为：

可以证明，n次Bezier矩阵还可以表示为递推的形式：

下列程式码为一简单的实际运用范例，展示如何使用C标出三次方贝塞尔曲线。注意，此处仅简单的计算多项式系数，并读尽一系列由0至1的t值；实践中一般不会这么做，递归求解通常会更快速——以更多的内存为代价，花费较少的处理器时间。不过直接的方法较易于理解并产生相同结果。以下程式码已使运算更为清晰。实践中的最佳化会先计算系数一次，并在实际计算曲线点的循环中反复使用。此处每次都会重新计算，损失了效率，但程式码更清楚易读。

曲线的计算可在曲线阵列上将相连点画上直线——点越多，曲线越平滑。

在部分架构中，下以程式码也可由动态规划进行最佳化。举例来说，dt是一个常数，cx * t则等同于每次反复就修改一次常数。经反复应用这种最佳化后，循环可被重写为没有任何乘法（虽然这个过程不是稳定数值的）。

/*產生三次方貝茲曲線的程式碼
*/typedef struct
{float x;float y;
}
Point2D;/*cp在此是四個元素的陣列:cp[0]為起始點，或上圖中的P0cp[1]為第一個控制點，或上圖中的P1cp[2]為第二個控制點，或上圖中的P2cp[3]為結束點，或上圖中的P3t為參數值，0 <= t <= 1
*/Point2D PointOnCubicBezier( Point2D* cp, float t )
{float   ax, bx, cx;float   ay, by, cy;float   tSquared, tCubed;Point2D result;/*計算多項式係數*/cx = 3.0 * (cp[1].x - cp[0].x);bx = 3.0 * (cp[2].x - cp[1].x) - cx;ax = cp[3].x - cp[0].x - cx - bx;cy = 3.0 * (cp[1].y - cp[0].y);by = 3.0 * (cp[2].y - cp[1].y) - cy;ay = cp[3].y - cp[0].y - cy - by;/*計算位於參數值t的曲線點*/tSquared = t * t;tCubed = tSquared * t;result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x;result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y;return result;
}/*ComputeBezier以控制點cp所產生的曲線點，填入Point2D結構的陣列。呼叫者必須分配足夠的記憶體以供輸出結果，其為<sizeof(Point2D) numberOfPoints>
*/void ComputeBezier( Point2D* cp, int numberOfPoints, Point2D* curve )
{float   dt;int     i;dt = 1.0 / ( numberOfPoints - 1 );for( i = 0; i < numberOfPoints; i++)curve[i] = PointOnCubicBezier( cp, i*dt );
}

德卡斯特里奥算法（De Casteljau’s Algorithm）绘制贝塞尔曲线

德卡斯特里奥算法可以计算贝塞尔曲线上的点C(u)，u∈[0,1]。因此，通过给定一组u的值，便可以计算出贝塞尔曲线上的坐标序列，从而绘制出贝塞尔曲线。

德卡斯特里奥算法的基础就是在向量AB上选择一个点C，使得C分向量AB为u:1-u（也就是∣AC∣:∣AB∣= u）。给定点A、B的坐标以及u（u∈[0,1]）的值，点C的坐标便为：C = A + (B - A) * u = (1 - u) * A + B * u。

定义贝塞尔曲线的控制点P_i编号为0i，其中，0表示是第0次迭代。当第一、二、三……次迭代时，0将会被1、2、3……替换。

德卡斯特里奥算法的思想如下：为了计算n次贝塞尔曲线上的点C(u), u∈[0,1]，首先将控制点连接形成一条折线00-01-02……0(n - 1)-0n。利用上述方法，计算出折线中每条线段0j-0(j+1)上的一个点1j,使得点1j分该线段的比为u:1-u。然后在折线10-11-……-1(n-1)上递归调用该算法，以此类推。最终，求得最后一个点n0。德卡斯特里奥证明了，点n0一定是曲线上的点。

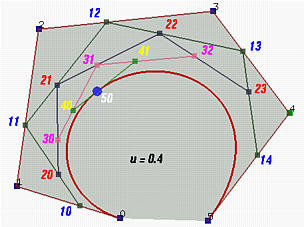
如上图，曲线控制点是00、01、02、03、04、05。线段00-01上取点10，10分该线段的比为u:1-u，类似地取点11、12、13、14，然后第二次迭代在线段10-11上取点20，点20分该线段的比为u:1-u，类似地取点21、22、23。然后进行下一次迭代，依次类推，直到最后在线段40-41上取点50，50是最终惟一的点，也是在曲线上的点。

上述直观的算法描述可以表达成一个计算方法。

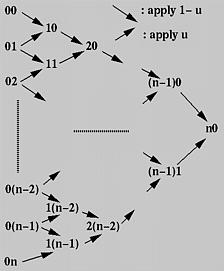
首先，将所有给定的控制点排列成一列，在上图中，即为最左边的一列。每一对相邻的控制点可以伸出两个箭头，分别指向右下方和右上方。在相邻箭头的交叉处，生成一个新的控制点。例如，控制点ij和i(j +1)生成新的控制点(i + 1)j。指向右下方的箭头表示乘以(1 - u)，指向右上方的箭头表示乘以u。

因此，通过第0列，可以求出第1列，然后求出第2列……，最终，在n次迭代后，可以到达惟一的一个点n0，这个点就是曲线上的点。

该计算过程算法如下：

Input: array P[0:n] of n+1 points and real number u in [0,1] Output: point on curve, C(u) Working: point array Q[0:n] for i := 0 to n do

Q[i] := P[i]; // save input

for k := 1 to n do

for i := 0 to n - k do

Q[i] := (1 - u)Q[i] + u Q[i + 1];

return Q[0];

该计算方法可以推导出一个递归关系：

但是，直接通过递归方法计算P_i,j效率低下，其原因与通过递归方法计算斐波那契数列一样：递归方法有大量的重复计算。

德卡斯特里奥算法还有一个有趣的性质。对于同一列中的连续的一组控制点，对其应用德卡斯特里奥算法，那么由这些控制点确定的曲线上的点，就是以这组控制点为边的等边三角形中，与这些控制点相对的顶点。

例如：由控制点02、03、04、05确定的曲线上的，对应u的点是32，正如下图中蓝色的等边三角形所表示的。同样，控制点11、12、13确定的曲线上的，对应u的点是31，如图，黄色三角形所示。

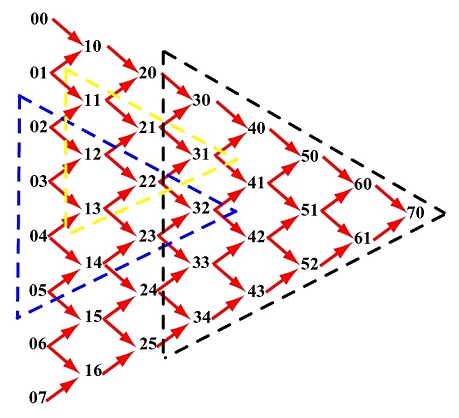
根据上面所述，通过给定一组u值，便可以计算出贝塞尔曲线上的坐标序列，从而绘制出贝塞尔曲线。

[csharp] view plain copy print ?

// arrayCoordinate为控制点
void CChildView::DrawBezier(CDC *pDC, const CArray<CPoint, CPoint>& arrayCoordinate)
{
int n = 0;
if((n = arrayCoordinate.GetSize()) < 2)
return;
double *xarray = new double[n - 1];
double *yarray = new double[n - 1];
double x = arrayCoordinate.GetAt(0).x;
double y = arrayCoordinate.GetAt(0).y;
for(double t = 0.0; t <=1; t += 0.05 / n) // 调整参数t,计算贝塞尔曲线上的点的坐标,t即为上述u
{
for(int i = 1; i < n; ++i)
{
for(int j = 0; j < n - i; ++j)
{
if(i == 1) // i==1时,第一次迭代,由已知控制点计算
{
xarray[j] = arrayCoordinate.GetAt(j).x * (1 - t) + arrayCoordinate[j + 1].x * t;
yarray[j] = arrayCoordinate.GetAt(j).y * (1 - t) + arrayCoordinate[j + 1].y * t;
continue;
}
// i != 1时,通过上一次迭代的结果计算
xarray[j] = xarray[j] * (1 - t) + xarray[j + 1] * t;
yarray[j] = yarray[j] * (1 - t) + yarray[j + 1] * t;
}
}
pDC->MoveTo(x, y);
pDC->LineTo(xarray[0], yarray[0]);
x = xarray[0];
y = yarray[0];
}
delete [] xarray;
delete [] yarray;
}

Bezier曲线原理相关推荐

Bezier曲线原理—动态解释
Bezier曲线原理贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线.一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由线段与节点组成,节点是可拖 ...
Bezier曲线原理及其代码实现
Bezier曲线原理及实现代码(c++) 一.原理: 贝塞尔曲线于1962年,由法国工程师皮埃尔?贝塞尔(Pierre B?zier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计.贝塞尔曲线最初 ...
Bezier曲线原理及实现代码（c++）
一.原理: 贝塞尔曲线于1962年,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计.贝塞尔曲线最初由 Paul de Casteljau 于 ...
bezier曲线解析与代码（c++）
前言: 作为rhino重度用户,我对于nurbs建模早有耳闻,但对于何为nurbs却不得其解.最近借上<计算机辅助设计>课程的机会,对此作了一些深入的学习,于是在此记录一下一些课程笔记和课 ...
android曲线位移动画,Bezier曲线在Android动画中的应用
Android动画的开发中,为了达到更加酷炫的效果,常常需要自定义运动轨迹,或者绘制花式复杂的曲线,这正是Bezier曲线大显神通的地方,本文将带你了解Bezier曲线在Android开发中的一些应用 ...
计算机图形学：三次Bezier曲线的绘制（算法原理及代码实现）
一.实现方案贝塞尔曲线原理:贝塞尔曲线是计算机图形图像造型的基本工具,是图形造型运用得最多的基本线条之一.它通过控制曲线上的四个点(起始点.终止点以及两个相互分离的中间点)来创造.编辑图形.其中起重 ...
Bezier曲线生成【计算机图形学】
原理: Bezier曲线是通过一组多边形折线的顶点来定义的.如果折线的顶点固定不变,则由其定义的Bezier曲线是唯一的.在折线的各顶点中,只有第一点和最后一点在曲线上且作为曲线的起始处和终止处,其他 ...
Bezier曲线、B样条和NURBS的基本概念
最不能理解的一点,一讨论软件的曲面,曲线功能,最后就变成曲线.曲面的数学原理的讨论了,但是里面也没数学好的,讨论的结果可想而知. 我不是数学家,我不懂这么复杂的方程,只要好用就行了. 在CAD中,设计 ...
【四足机器人--摆动相足端位置速度轨迹规划】（4.1）FootSwingTrajectory（bezier曲线计算脚的摆动轨迹）代码解析
系列文章目录提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理文章目录系列文章目录前言一.FootSwingTrajectory(bezier曲线)的内容 ...

Bezier曲线原理

一般化

德卡斯特里奥算法（De Casteljau’s Algorithm）绘制贝塞尔曲线

Bezier曲线原理相关推荐

最新文章

热门文章