变分法理解2——基本方法

本文是变分法理解系列的第2篇文章，第一篇文章见变分法理解1——泛函简介，本文的要点如下：

基本概念
两个引理
什么是函数的变分
什么是泛函的变分
欧拉-拉格朗日方程（Euler–Lagrange equation）的证明

基本概念

具有某种共同性质的函数构成的集合称为类函数，记作F。例如在最速降线例子中的所有曲线都通过点O和A，通过点O和A就是函数集合具有的共同性质。

如果一个类函数中的某个函数能够使某个泛函取得极值或可能取得极值，则该类函数称为变分问题的可取类函数。可取类函数中的函数有无穷多个，其中任何一个都称为可取函数。

类函数中能使泛函取得极值或可能取得极值的函数或曲线称为极值函数，也称为变分问题的解。

变分法的核心问题就是求解泛函的极值函数和极值函数对应的泛函极值。

如果可取曲线类的曲线端点预先给出且为定值，则所求泛函极值的问题称为固定端点变分问题。

引理

引理1

如果函数 f(x)f(x)f(x) 在[a,b][a,b][a,b]内连续， η(x)\eta(x)η(x) 是满足 η(a)=η(b)=0\eta(a)=\eta(b)=0η(a)=η(b)=0 的任意函数，如果

∫abf(x)η(x)dx=0\int_a^b f(x)\eta(x)dx=0 ∫abf(x)η(x)dx=0

成立，那么对于所有的x∈[a,b]x\in[a,b]x∈[a,b],有f(x)≡0f(x)\equiv0f(x)≡0

证明：

反证法，设f(x)不恒为0

由 η(x)\eta(x)η(x) 的任意性，取 η(x)=−f(x)(x−a)(x−b)\eta(x)=-f(x)(x-a)(x-b)η(x)=−f(x)(x−a)(x−b) ，xxx是aaa和bbb之间变动的变量，所以(x−a)(x−b)(x-a)(x-b)(x−a)(x−b)为负，由f(xf(xf(x)不恒为0，有：

∫abf(x)η(x)dx=∫ab−f(x)2(x−a)(x−b)>0\int_a^b f(x)\eta(x)dx=\int_a^b-f(x)^2 (x-a)(x-b)>0 ∫abf(x)η(x)dx=∫ab−f(x)2(x−a)(x−b)>0

与条件矛盾，所以f(x)≡0f(x)\equiv0f(x)≡0

引理2

如果函数 f(x),g(x)f(x),g(x)f(x),g(x)在[a,b][a,b][a,b]内连续， η(x),ξ(x)\eta(x),\xi(x)η(x),ξ(x) 是满足 η(a)=η(b)=0\eta(a)=\eta(b)=0η(a)=η(b)=0 且 ξ(a)=ξ(b)=0\xi(a)=\xi(b)=0ξ(a)=ξ(b)=0 的任意函数，如果

∫ab[f(x)η(x)+g(x)ξ(x)]dx=0\int_a^b[f(x)\eta(x)+g(x)\xi(x)]dx=0 ∫ab[f(x)η(x)+g(x)ξ(x)]dx=0

成立，那么对于所有的 x∈[a,b]x \in [a,b]x∈[a,b] ，有 f(x)≡g(x)≡0f(x) \equiv g(x) \equiv 0f(x)≡g(x)≡0 。

证明：

反证法，设f(x)和g(x)不恒为0

由 η(x),ξ(x)\eta(x),\xi(x)η(x),ξ(x) 的任意性，取 η(x)=−f(x)(x−a)(x−b),ξ(x)=−g(x)(x−a)(x−b)\eta(x)=-f(x)(x-a)(x-b),\xi(x)=-g(x)(x-a)(x-b)η(x)=−f(x)(x−a)(x−b),ξ(x)=−g(x)(x−a)(x−b)，xxx是aaa和bbb之间变动的变量，所以(x−a)(x−b)(x-a)(x-b)(x−a)(x−b)为负，则：

∫ab[f(x)η(x)+g(x)ξ(x)]dx=∫ab[f(x)2+g(x)2][−(x−a)(x−b)]dx>0\int_a^b[f(x)\eta(x)+g(x)\xi(x)]dx=\int_a^b[f(x)^2+g(x)^2][-(x-a)(x-b)]dx>0 ∫ab[f(x)η(x)+g(x)ξ(x)]dx=∫ab[f(x)2+g(x)2][−(x−a)(x−b)]dx>0

这与条件矛盾，所以f(x)≡g(x)≡0f(x)\equiv g(x) \equiv0f(x)≡g(x)≡0

函数的变分

对于任意定值 x∈[x0,x1]x \in [x_0,x_1]x∈[x0,x1] ，可取函数y(x)y(x)y(x) 与另一可取函数 y0(x)y_0(x)y0(x)之差 y(x)−y0(x)y(x)-y_0(x)y(x)−y0(x) 称为函数y(x)y(x)y(x) 在 y0(x)y_0(x)y0(x)处的变分或者叫函数的变分，记作 δy\delta yδy ，其中 δ\deltaδ 称为变分算子，那么

δy=y(x)−y0(x)=ϵη(x)\delta y=y(x)-y_0(x)=\epsilon\eta(x) δy=y(x)−y0(x)=ϵη(x)

关于 ϵη(x)\epsilon \eta(x)ϵη(x) 下文会详细讲

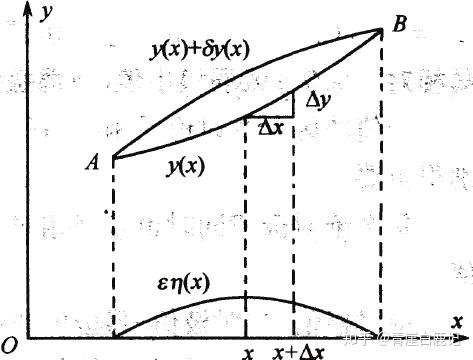
这里注意一下函数的变分 δy\delta yδy 与函数的增量Δy\Delta yΔy 之间的区别，如图所示

函数的变分 δy\delta yδy 是两个不同的函数y(x)y(x)y(x) 和y0(x)y_0(x)y0(x) 在自变量x固定时的差，这是函数发生了改变。
函数的增量 Δy\Delta yΔy 是自变量x的增量使得函数 y(x)y(x)y(x) 产生的增量，函数依然是原来的函数。

最简泛函的变分

设 F(x,y(x),y′(x))F(x,y(x),y'(x))F(x,y(x),y′(x)) 是三个独立变量 x,y(x),y′(x)x,y(x),y'(x)x,y(x),y′(x) 在区间 [x0,x1][x_0,x_1][x0,x1] 上的已知函数，且二阶连续可微，其中 y(x)y(x)y(x) 和 y′(x)y'(x)y′(x) 是xxx的未知函数，则泛函：

J[y(x)]=∫x0x1F(x,y(x),y′(x))dxJ[y(x)]=\int_{x_{0}}^{x_{1}}F(x,y(x),y'(x))dx J[y(x)]=∫x0x1F(x,y(x),y′(x))dx

被称为最简泛函，被积函数F成为泛函的核。

在 y=y(x)y=y(x)y=y(x) 的一阶邻域内，任取一曲线 y=y1(x)y=y_1(x)y=y1(x) ，则：

δy=y1(x)−y(x),δy′=y1′(x)−y′(x)\delta y=y_1(x)-y(x),\delta_y'=y'_1(x)-y'(x) δy=y1(x)−y(x),δy′=y1′(x)−y′(x)

由泰勒展开式，最简泛函 J[y(x)]J[y(x)]J[y(x)]的增量为：

△J=J[y1(x)]−J[y(x)]=J[y(x)+δy]−J[y(x)]=∫x0x1[F(x,y)+δy,y′+δy′)dx−∫x0x1F(x,y,y′)dx=∫x0x1[F(x,y+δy,y′+δy′)−F(x,y,y′)]dx=∫x0x1(Fyδy+Fy′δy′)dx+⋯+∫x0x1[1n!(δy∂∂y+δy′∂∂y′)nF]dx+Rn\begin{aligned} \triangle J&=J[y_1(x)]-J[y(x)]=J[y(x)+\delta y]-J[y(x)] \\ &=\int_{x_0}^{x_1}[F(x,y)+\delta y,y'+\delta y')dx-\int_{x_0}^{x_1}F(x,y,y')dx\\ &=\int_{x_0}^{x_1}[F(x,y+\delta y,y'+\delta y')-F(x,y,y')]dx\\ &=\int_{x_0}^{x_1}(F_y\delta y+F_{y'}\delta y')dx+\cdots+\int_{x_0}^{x_1}[\frac{1}{n!}(\delta y \frac{\partial}{\partial y}+\delta y'\frac{\partial}{\partial y'})^{n}F]dx+R_{n} \end{aligned} △J=J[y1(x)]−J[y(x)]=J[y(x)+δy]−J[y(x)]=∫x0x1[F(x,y)+δy,y′+δy′)dx−∫x0x1F(x,y,y′)dx=∫x0x1[F(x,y+δy,y′+δy′)−F(x,y,y′)]dx=∫x0x1(Fyδy+Fy′δy′)dx+⋯+∫x0x1[n!1(δy∂y∂+δy′∂y′∂)nF]dx+Rn

把∫x0x1(Fyδy+Fy′δy′)dx\int_{x_0}^{x_1}(F_y\delta y+F_{y'}\delta y')dx∫x0x1(Fyδy+Fy′δy′)dx 称为泛函的变分，记作 δJ\delta JδJ

Euler–Lagrange equation

回顾变分法理解1——泛函简介中的最速降线问题：

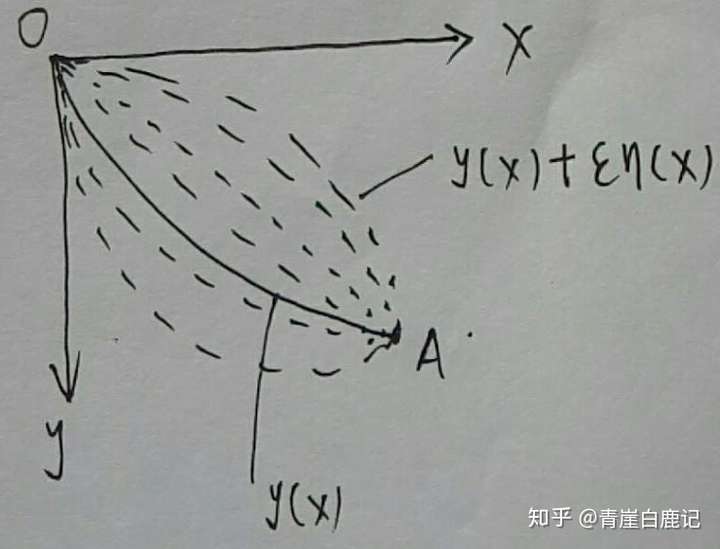
设 y~(x)\tilde y(x)y~(x) 是一个可取类函数，即图中所有实线和虚线的集合。

在可取类函数 y~(x)\tilde y(x)y~(x) 中存在一个二阶可微的极值函数y(x)y(x)y(x)（图中的实线）使得重物从O到A点的时间最短，即y(x)y(x)y(x)可以使泛函 t=J[y~(x)]=∫0a(1+(y~)′2)2gy~dx\displaystyle t=J[\tilde y(x)]=\int_0^a \sqrt{\frac{(1 + (\tilde y)'^2)}{2g \tilde y}}dxt=J[y~(x)]=∫0a2gy~(1+(y~)′2)dx 取得极值。

可以用y(x)表示可取类函数中的所有曲线：

y~(x)=y(x)+δy=y(x)+ϵη(x)\tilde y(x)=y(x)+\delta y=y(x)+\epsilon\eta(x) y~(x)=y(x)+δy=y(x)+ϵη(x)

其中 ϵ\epsilonϵ 为Lagrange引入的实数， η(x)\eta(x)η(x) 是满足 η(x0)=η(x1)=0\eta(x_0)=\eta(x_1)=0η(x0)=η(x1)=0 的可微函数，可以看出在 ϵ=0\epsilon=0ϵ=0 时 y~(x)=y(x)\tilde{y}(x)= y(x)y~(x)=y(x) ，使泛函 t=J[y~(x)]=∫0a(1+(y~)′2)2gy~dx\displaystyle t=J[\tilde y(x)]=\int_0^a \sqrt{\frac{(1 + (\tilde y)'^2)}{2g \tilde y}}dxt=J[y~(x)]=∫0a2gy~(1+(y~)′2)dx 取得极值为 J[y(x)]J[y(x)]J[y(x)]。

泛函 J[y~(x)]J[\tilde y(x)]J[y~(x)] 可以表示为：

ϕ(ϵ)=J[y~(x)]=J[y(x)+ϵη(x)]=∫x0x1F(x,y(x)+ϵη(x),y′(x)+ϵη′(x))dx\phi(\epsilon)=J[\tilde y(x)]=J[y(x)+\epsilon\eta(x)]=\int_{x_0}^{x_1}F(x,y(x)+\epsilon\eta(x),y'(x)+\epsilon\eta'(x))dx ϕ(ϵ)=J[y~(x)]=J[y(x)+ϵη(x)]=∫x0x1F(x,y(x)+ϵη(x),y′(x)+ϵη′(x))dx

式是一个关于 x 积分式，在求解积分之后，剩下的只有 ϵ\epsilonϵ ，因此它其实是 ϵ\epsilonϵ 的函数，这个函数的特性是在ϵ=0\epsilon=0ϵ=0 时取得极值J[y(x)]J[y(x)]J[y(x)]，也就是在 ϵ=0\epsilon=0ϵ=0 时， ϕ(ϵ)\phi(\epsilon)ϕ(ϵ) 满足：

dϕdϵ∣ϵ=0=0\frac{d\phi}{d\epsilon}|_{\epsilon=0}=0 dϵdϕ∣ϵ=0=0

由求导与积分顺序的可交换性， dϕdϵ\displaystyle \frac{d \phi}{d \epsilon}dϵdϕ 形式如下：

dϕdϵ=∫x0x1Fy[x,y(x)+ϵη(x),y′(x)+ϵη′(x)]η(x)+Fy′[x,y(x)+ϵη(x),y′(x)+ϵη′(x)]η′(x)dx\frac{d\phi}{d\epsilon}=\int_{x_0}^{x_1}F_y[x,y(x)+\epsilon\eta(x),y'(x)+\epsilon\eta'(x)]\eta(x)\\+F_{y'}[x,y(x)+\epsilon\eta(x),y'(x)+\epsilon\eta'(x)]\eta'(x)dx dϵdϕ=∫x0x1Fy[x,y(x)+ϵη(x),y′(x)+ϵη′(x)]η(x)+Fy′[x,y(x)+ϵη(x),y′(x)+ϵη′(x)]η′(x)dx

令 ϵ=0\epsilon=0ϵ=0 ：

dϕdϵ∣ϵ=0=∫x0x1[Fyη(x)+Fy′η′(x)]dx=0\frac{d\phi}{d\epsilon}|_{\epsilon=0}=\int_{x_0}^{x_1}[F_{y}\eta(x)+F_{y'}\eta'(x)]dx=0 dϵdϕ∣ϵ=0=∫x0x1[Fyη(x)+Fy′η′(x)]dx=0

应用分部积分法

0=∫x0x1[Fyη(x)+Fy′η′(x)]dx=∫x0x1Fyη(x)dx+∫x0x1Fy′η′(x)dx=Fyη(x)dx+∫x0x1Fy′dη(x)=Fyη(x)dx+Fy′η(x)∣x0x1−∫x0x1η(x)(ddxF′y)dx=∫x0x1(Fy−ddxF′y)η(x)dx+Fy′η(x)∣x0x1\begin{aligned} 0&=\int_{x_0}^{x_1}[F_y\eta(x)+F_{y'}\eta'(x)]dx\\ &=\int_{x_0}^{x_1}F_y\eta(x)dx+\int_{x_0}^{x_1}F_{y'}\eta'(x)dx\\ &=F_y\eta(x)dx+\int_{x_0}^{x_1}F_{y'}d\eta(x)\\ &=F_y\eta(x)dx+F_{y'}\eta(x)|_{x_0}^{x_1}-\int_{x_0}^{x_1}\eta(x)(\frac{d}{dx}F'y)dx\\ &=\int_{x_0}^{x_1}(F_y-\frac{d}{dx}F'y)\eta(x)dx+F_{y'}\eta(x)|_{x_0}^{x_1} \end{aligned} 0=∫x0x1[Fyη(x)+Fy′η′(x)]dx=∫x0x1Fyη(x)dx+∫x0x1Fy′η′(x)dx=Fyη(x)dx+∫x0x1Fy′dη(x)=Fyη(x)dx+Fy′η(x)∣x0x1−∫x0x1η(x)(dxdF′y)dx=∫x0x1(Fy−dxdF′y)η(x)dx+Fy′η(x)∣x0x1

由于 η(x0)=η(x1)=0\eta(x_0)=\eta(x_1)=0η(x0)=η(x1)=0 ，因此： Fy′η(x)∣x0x1=0F_{y'}\eta(x)|_{x_0}^{x_1}=0Fy′η(x)∣x0x1=0

推出：

∫x0x1(Fy−ddxF′y)η(x)dx\int_{x_0}^{x_1}(F_y-\frac{d}{dx}F'y)\eta(x)dx ∫x0x1(Fy−dxdF′y)η(x)dx

再由引理1：

Fy−ddxF′y=0F_y-\frac{d}{dx}F'y=0 Fy−dxdF′y=0
这就是Euler–Lagrange equation。

Euler–Lagrange equation也可以利用泛函取得极值时， δJ=0\delta J=0δJ=0 来证明。

η(x)\eta(x)η(x) 实际上是加在y(x)上一个扰动，Euler–Lagrange equation的意义在于不管扰动是什么形式，如果泛函取得极值，都有 Fy−ddxFy′=0\displaystyle F_y-\frac{d}{dx}F'_y=0Fy−dxdFy′=0成立。

转载自：
博主：清雅的数学笔记
博客地址：https://zhuanlan.zhihu.com/p/41810184
来源：知乎

变分法理解2——基本方法相关推荐

机器学习：一步步教你理解反向传播方法
机器学习:一步步教你理解反向传播方法时间 2016-09-13 00:35:59 Yong Yuan's blog 原文 http://yongyuan.name/blog/back-propa ...
behavior php,YII2框架中behavior行为的理解与使用方法示例
本文实例讲述了YII2框架中behavior行为的理解与使用方法.分享给大家供大家参考,具体如下: YII2中的行为说白了就是对组件功能的扩展,在不改变继承关系的条件下. 行为附加到组件后,行为将注入 ...
【数据清洗】异常点的理解与处理方法（1）
[数据清洗]异常点的理解与处理方法(1) 参考文章: (1)[数据清洗]异常点的理解与处理方法(1) (2)https://www.cnblogs.com/SevnChen/p/5024644.htm ...
从MIXMAX概率模型理解Bayesian建模方法
从MIXMAX概率模型理解Bayesian建模方法储备知识 HMM-隐马尔可夫模型(Hidden Markov Model) GMM-混合高斯模型多元高斯分布(The Multivariate n ...
理解WebViewClient各方法重写的作用
创建并设置一个WebViewClient子类,回调对应的方法改变网页内容的呈现方式,比如:网页加载错误回调onReceivedError(),提交表单错误回调onFormResubmission(), ...
深入理解Objective-C：方法缓存
摘要只要用到Objective-C,我们每天都会跟方法调用打交道.我们都知道Objective-C的方法决议是动态的,但是在底层一个方法究竟是怎么找到的,方法缓存又是怎么运作的却鲜为人知.本文主要从 ...
python递归详解_Python理解递归的方法总结
递归一个函数在执行过程中一次或多次调用其本身便是递归,就像是俄罗斯套娃一样,一个娃娃里包含另一个娃娃. 递归其实是程序设计语言学习过程中很快就会接触到的东西,但有关递归的理解可能还会有一些遗漏,下面 ...
深入理解 Objective-C：方法缓存
摘要只要用到Objective-C,我们每天都会跟方法调用打交道.我们都知道Objective-C的方法决议是动态的,但是在底层一个方法究竟是怎么找到的,方法缓存又是怎么运作的却鲜为人知.本文主要从 ...
Thread线程的深刻理解和代理方法参数[有图有真相]
在这说的是Thread的基本用法,线程池ThreadPool在这就不说的,以前的blog有写,基本上两个用法都是相同的.基本用法和图,不需要的大鸟请绕行,谢谢! 目录: 1.Thread基本用法与异步 ...

变分法理解2——基本方法

变分法理解2——基本方法相关推荐

最新文章

热门文章