脊回归（Ridge Regression）

标签：监督学习

@ author : duanxxnj@163.com
@ time : 2016-06-19

在《线性回归（Linear Regression）》中提到过，当使用最小二乘法计算线性回归模型参数的时候，如果数据集合矩阵（也叫做设计矩阵(design matrix)） X X，存在多重共线性，那么最小二乘法对输入变量中的噪声非常的敏感，其解会极为不稳定。为了解决这个问题，就有了这一节脊回归（Ridge Regression ）。

当设计矩阵XX存在多重共线性的时候（数学上称为病态矩阵），最小二乘法求得的参数 w w在数值上会非常的大，而一般的线性回归其模型是 y=wTxy=w^Tx ，显然，就是因为 w w在数值上非常的大，所以，如果输入变量xx有一个微小的变动，其反应在输出结果上也会变得非常大，这就是对输入变量总的噪声非常敏感的原因。

如果能限制参数 w w的增长，使ww不会变得特别大，那么模型对输入 w w中噪声的敏感度就会降低。这就是脊回归和套索回归（Ridge Regression and Lasso Regrission）的基本思想。

为了限制模型参数ww的数值大小，就在模型原来的目标函数上加上一个惩罚项，这个过程叫做正则化（Regularization）。

如果惩罚项是参数的 l2 l_{2}范数，就是脊回归(Ridge Regression)

如果惩罚项是参数的 l1 l_{1}范数，就是套索回归（Lasso Regrission）

正则化同时也是防止过拟合有效的手段，这在“多项式回归”中有详细的说明。

脊回归(Ridge Regression)

所谓脊回归，就是对于一个线性模型，在原来的损失函数加入参数的 l2 l_{2}范数的惩罚项，其损失函数为如下形式:

Jw=minw{||Xw−y||2+α||w||2}

J_{w}=\min_{w}\{\left|| Xw-y \right||^2+\alpha\left|| w \right||^2\}

这里 α \alpha是平法损失和正则项之间的一个系数， α≥0 \alpha \geq 0。

α \alpha的数值越大，那么正则项，也是惩罚项的作用就越明显； α \alpha的数值越小，正则项的作用就越弱。极端情况下， α=0 \alpha = 0则和原来的损失函数是一样的，如果 α=∞ \alpha = \infty，则损失函数只有正则项，此时其最小化的结果必然是 w=0 w=0。

关于alpha的数值具体的选择，归于“模型选择”章节，具体的方法可以参见“模型选择”。

其实，这个式子和拉格朗日乘子法的结果差不多，如果逆用拉格朗日乘子法的话，那么，上面的损失函数可以是下面的这种优化模型：

Jw=minw{||Xw−y||2}||w||2≤t

\begin{aligned} J_{w} =\min_{w}\{\left|| Xw-y \right||^2\}\\\left|| w \right||^2 \leq t \end{aligned}

在《线性回归》中，给出了线性回归的损失函数可以写为：

∥Xw−y∥2=(Xw−y)T(Xw−y)

\left \| Xw-y \right \|^{2}=(Xw-y)^T(Xw-y)

关于参数 w w求导之后：

XT(Xw−y)+XT(Xw−y)=0

X^T(Xw-y) + X^T(Xw-y)=0

其解为：

w=(XTX)−1XTy

w=(X^TX)^{-1}X^Ty

这里，脊回归的损失函数为：

∥Xw−y∥2+α||w||2=(Xw−y)T(Xw−y)+αwTw

\left \| Xw-y \right \|^{2} +\alpha\left|| w \right||^2 =(Xw-y)^T(Xw-y)+\alpha w^Tw

关于参数 w w求导之后：

XT(Xw−y)+XT(Xw−y)+αw=0

X^T(Xw-y) + X^T(Xw-y) + \alpha w=0

其解为：

w=(XTX+αI)−1XTy

w=(X^TX+\alpha I)^{-1}X^Ty

下面给出一个脊回归简单的代码示例，这个代码显示了不同的alpha对模型参数 w w的影响程度。alpha越大，则ww的数值上越小；alpha越小，则 w <script type="math/tex" id="MathJax-Element-66">w</script>的数值上越大，注意所生成的图片为了更好的观察，将x轴做了反转。

#!/usr/bin/python
# -*- coding: utf-8 -*-"""
author ： duanxxnj@163.com
time : 2016-06-03-14-34脊回归测试代码
这里需要先生成一个线性相关的设计矩阵X，再使用脊回归对其进行建模
脊回归中最重要的就是参数alpha的选择，本例显示了不同的alpha下
模型参数omega不同的结果"""print(__doc__)import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model# 这里设计矩阵X是一个希尔伯特矩阵（Hilbert matrix）
# 其元素A（i,j）=1(i + j -1),i和j分别为其行标和列标
# 希尔伯特矩阵是一种数学变换矩阵，正定，且高度病态
# 即，任何一个元素发生一点变动，整个矩阵的行列式的值和逆矩阵都会发生巨大变化
# 这里设计矩阵是一个10x5的矩阵，即有10个样本，5个变量
X = 1. / (np.arange(1, 6) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)print '设计矩阵为：'
print X# alpha 取值为10^（-10）到10^（-2）之间的连续的200个值
n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
print '\n alpha的值为：'
print alphas# 初始化一个Ridge Regression
clf = linear_model.Ridge(fit_intercept=False)# 参数矩阵，即每一个alpha对于的参数所组成的矩阵
coefs = []
# 根据不同的alpha训练出不同的模型参数
for a in alphas:clf.set_params(alpha=a)clf.fit(X, y)coefs.append(clf.coef_)# 获得绘图句柄
ax = plt.gca()
# 参数中每一个维度使用一个颜色表示
ax.set_color_cycle(['b', 'r', 'g', 'c', 'k'])# 绘制alpha和对应的参数之间的关系图
ax.plot(alphas, coefs)
ax.set_xscale('log')    #x轴使用对数表示
ax.set_xlim(ax.get_xlim()[::-1])  # 将x轴反转，便于显示
plt.grid()
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()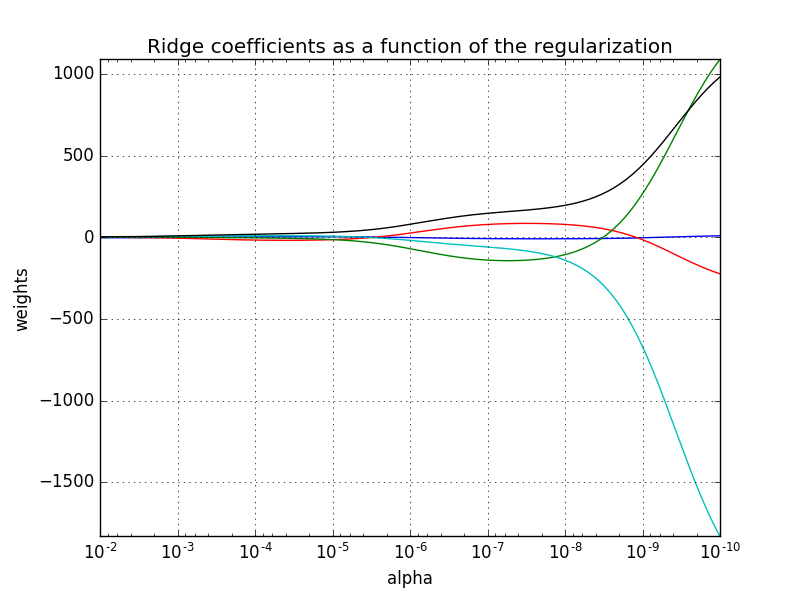

基于交叉验证的脊回归

在前面提到过，脊回归中，alpha的选择是一个比较麻烦的问题，这其实是一个模型选择的问题，在模型选择中，最简单的模型选择方法就是交叉验证（Cross-validation），将交叉验证内置在脊回归中，就免去了alpha的人工选择，其具体实现方式如下：

#!/usr/bin/python
# -*- coding: utf-8 -*-"""
author ： duanxxnj@163.com
time : 2016-06-19-20-59基于交叉验证的脊回归alpha选择
可以直接获得一个相对不错的alpha"""print(__doc__)import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model# 这里设计矩阵X是一个希尔伯特矩阵（Hilbert matrix）
# 其元素A（i,j）=1(i + j -1),i和j分别为其行标和列标
# 希尔伯特矩阵是一种数学变换矩阵，正定，且高度病态
# 即，任何一个元素发生一点变动，整个矩阵的行列式的值和逆矩阵都会发生巨大变化
# 这里设计矩阵是一个10x5的矩阵，即有10个样本，5个变量
X = 1. / (np.arange(1, 6) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)print '设计矩阵为：'
print X# 初始化一个Ridge Cross-Validation Regression
clf = linear_model.RidgeCV(fit_intercept=False)# 训练模型
clf.fit(X, y)print
print 'alpha的数值 : ', clf.alpha_
print '参数的数值：', clf.coef_

其运行结果如下：

设计矩阵为：
[[ 1.          0.5         0.33333333  0.25        0.2       ][ 0.5         0.33333333  0.25        0.2         0.16666667][ 0.33333333  0.25        0.2         0.16666667  0.14285714][ 0.25        0.2         0.16666667  0.14285714  0.125     ][ 0.2         0.16666667  0.14285714  0.125       0.11111111][ 0.16666667  0.14285714  0.125       0.11111111  0.1       ][ 0.14285714  0.125       0.11111111  0.1         0.09090909][ 0.125       0.11111111  0.1         0.09090909  0.08333333][ 0.11111111  0.1         0.09090909  0.08333333  0.07692308][ 0.1         0.09090909  0.08333333  0.07692308  0.07142857]]alpha的数值 :  0.1
参数的数值： [-0.43816548  1.19229228  1.54118834  1.60855632  1.58565451]

脊回归（Ridge Regression）相关推荐

脊回归(Ridge Regression) 岭回归
岭回归(英文名:ridge regression, Tikhonov regularization)是一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的 ...
多元线性回归算法: 线性回归Linear Regression、岭回归Ridge regression、Lasso回归、主成分回归PCR、偏最小二乘PLS
0. 问题描述输入数据:X=(x1,x2,....,xm)\mathbf{X} = (x_1, x_2,...., x_m)X=(x1,x2,....,xm), 相应标签 Y=(y1,y2,. ...
岭回归(Ridge Regression)和Lasso回归
1.岭回归(Ridge Regression) 标准线性回归(简单线性回归)中: 如果想用这个式子得到回归系数,就要保证(X^TX)是一个可逆矩阵. 下面的情景:如果特征的数据比样本点还要多,数据特征 ...
Basics Algorithms| 岭回归(Ridge regression)
Ridge Regression is a linear regression with L2 regularization. 1. 线性回归(Linear Regression, LR) LR就是用 ...
从最小二乘到岭回归(Ridge Regression)的深刻理解
岭回归是带二范数惩罚的最小二乘回归. ols方法中, &lt;img src="https://pic1.zhimg.com/716fd592b5b8cb384bd68771 ...
岭回归(Ridge Regression)
岭回归出现的原因: 为了求得参数w,也可以不用迭代的方法(比如梯度下降法对同一批数据一直迭代,可以采用标准方程法一次性就算出了w = (XTX)-1XTy ,但是如果数据的特征比样本点还多,则计算(X ...
套索回归 (Lasso Regression)的基本应用
一.使用场合与岭回归类似,套索 (Least Absolute Shrinkage and Selection Operator) 也会对回归系数的绝对值添加一个罚值.此外,它能降低偏差并提高线性回 ...
R语言使用caret包构建岭回归模型（Ridge Regression ）构建回归模型、通过method参数指定算法名称、通过trainControl函数控制训练过程
R语言使用caret包构建岭回归模型(Ridge Regression )构建回归模型.通过method参数指定算法名称.通过trainControl函数控制训练过程目录
R语言glmnet拟合岭回归模型实战：岭回归模型的模型系数（ridge regression coefficients）及可视化、岭回归模型分类评估计算（混淆矩阵、accuracy、Deviance)
R语言glmnet拟合岭回归模型(ridge regression)实战:岭回归模型的模型系数(ridge regression coefficients)及可视化.岭回归模型分类评估计算(混淆矩阵. ...

脊回归（Ridge Regression）

脊回归（Ridge Regression）

脊回归(Ridge Regression)

基于交叉验证的脊回归

脊回归（Ridge Regression）相关推荐

最新文章

热门文章