Supervised Descent Method(人脸对齐之SDM论文解析）

Supervised Descent Method(人脸对齐之SDM论文解析）

标签： SDM NLS Jacobian Hessian FaceAlignment

作者：贾金让
本人博客链接:http://blog.csdn.net/jiajinrang93

1.概述

文章名称：Supervised Descent Method and its Applications to Face Alignment
文章来源：2013CVPR
文章作者：Xuehan Xiong，Fernando De la Torre
简要介绍：这篇文章主要提出了一种名为SDM（Supervised Descent Method）的方法，用来最小化非线性最小二乘（Non-linear Least Squares）目标函数，即目标函数是均方误差。SDM方法通过学习得到一系列下降的方向和该方向上的尺度，使得目标函数以非常快的速度收敛到最小值，回避了求解Jacobian矩阵和Hessian矩阵的问题。下面开始详细介绍，我补充了文章中只给出结果的推导过程，并且稍微调整了一下文章中牛顿步的推导过程。

2.从牛顿步说起

数值优化在很多领域都有很重要的应用，计算机视觉中很多重要的问题比如（行人跟踪、人脸对齐等）都可以化成非线性优化问题来解决。解决非线性优化的方法有很多，其中非常常用的有基于一阶的或者是二阶的优化方法，比如梯度下降方法、牛顿步、LM算法等等。尽管很多年过去了，在二阶导可求得情况下，牛顿步仍然被认为是一个非常优秀的算法。

那么什么是牛顿步方法呢？下面简单介绍一下牛顿步，后面还会详细推导牛顿步。

牛顿步：在Hessian矩阵正定的情况下，极小值可以通过求解线性方程组来迭代求解。给定一个初始的估计值x0∈ℜp×1x_0\in\Re^{p\times1}x0∈ℜp×1，牛顿步的更新迭代公式如下：
xk+1=xk−H−1(xk)Jf(xk)(1)x_{k+1}=x_k-H^{-1}(x_k)J_f(x_k)\tag{1}xk+1=xk−H−1(xk)Jf(xk)(1)
其中H−1(xk)∈ℜp×pH^{-1}(x_k)\in\Re^{p\times p}H−1(xk)∈ℜp×p是在xkx_kxk点的Hessian矩阵,Jf(xk)∈ℜp×1J_f(x_k)\in\Re^{p\times1}Jf(xk)∈ℜp×1是在xkx_kxk点的 Jacobian矩阵。
牛顿步方法有两个主要优点：

如果牛顿步可以收敛，那么它的收敛速度是二次的，收敛速度非常快。
如果初始点在最小点邻域附近，那么它一定可以收敛。
但牛顿法在应用中，也有几个缺点：
Hessian矩阵在极小值附近是局部正定的，但可能不是全局正定的，这就会导致牛顿步并不一定朝向下降的方向。
牛顿步需要函数二次可导。这个要求在实际应用中是一个很强的要求，比如图像处理中经常被使用的SIFT特征，它可以被看成是一个不可导的特征，因此在这种情况下，在我们只能通过数值逼近下降的方向或者是Hessian矩阵，但这种计算代价非常大。
由于Hessian矩阵通常很大，计算它的逆矩阵代价是非常大的，复杂度通常是O(p3)O(p^3)O(p3)。
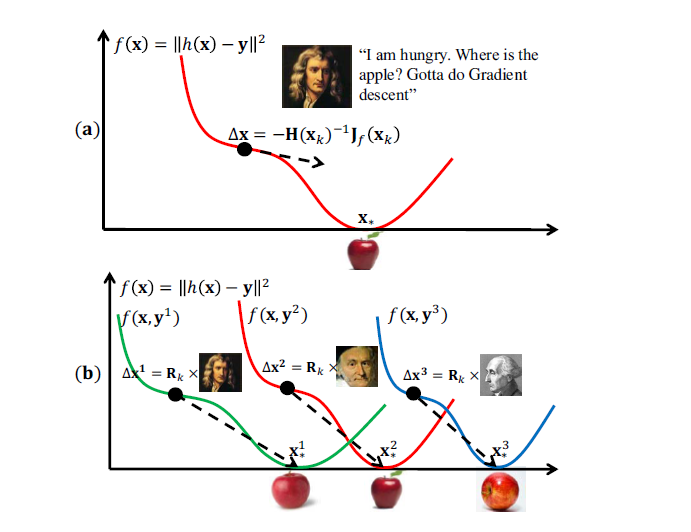
以上三个缺陷使我们在实际应用中，很难计算精确的Hessian矩阵，甚至连数值逼近都是很困难的（由于计算代价比较大）。因此，该文章提出了SDM方法，用数据来学习下降的方向。下面两张图可以用来初步表示牛顿步和SDM两种方法的基本原理。

3.人脸对齐的几个概念（简单介绍）

在介绍SDM之前，还要先简单提一下人脸识别中人脸对齐的基本原理和相关的关键词，因为该SDM方法主要是在人脸对齐方面进行应用。
人脸对齐（Face Alignment）基本原理：
基本概念：人脸识别（face recognizaton）按顺序可以大体上分为四个部分，即人脸检测（face detection),人脸对齐（face alignment），人脸校验（face verification）和人脸识别（face identification）。人脸检测就是在一张图片中找到人脸所处的位置，即将人脸圈出来，比如拍照时数码相机自动画出人脸。人脸对齐就是在已经检测到的人脸的基础上，自动找到人脸上的眼睛鼻子嘴和脸轮廓等标志性特征位置。人脸校验就是判断两张脸是不是同一个人。人脸识别就是给定一张脸，判断这张脸是谁。
本文研究其中的第二部分，人脸对齐。
人脸对齐中的几个关键词：
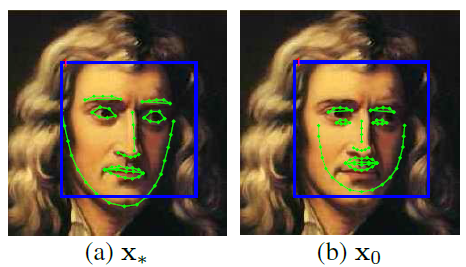
形状（shape）：形状就是人脸上的有特征的位置，如下图所示，每张图中所有黄点构成的图形就是该人脸的形状。
特征点（landmark）：形状由特征点组成，图中的每一个黄点就是一个特征点。

人脸对齐的最终目的就是在已知的人脸方框（一般由人脸检测确定人脸的位置）上定位其准确地形状。
人脸对齐的算法主要分为两大类：基于优化的方法（Optimization-based method）和基于回归的方法（Regression-based method）。
SDM方法属于基于回归的方法。
基于回归的方法的基本原理：对于一张给定的人脸，给出一个初始的形状，通过不断地迭代，将初始形状回归到接近甚至等于真实形状的位置。

4.Supervised Descent Method

给定一张含有m个像素的图片d∈ℜm×1d\in\Re^{m\times1}d∈ℜm×1,d(x)∈ℜp×1d(x)\in\Re^{p\times1}d(x)∈ℜp×1表示该图片上的p个特征点，h()h()h()表示一个非线性特征提取函数，比如h(d(x))∈ℜ128p×1h(d(x))\in\Re^{128p\times1}h(d(x))∈ℜ128p×1可以表示从p个特征点上提取出的SIFT特征，每个特征点提取出了128个SIFT特征。那么我们的目标就是，在给定一个初始形状x0x_0x0的基础上，通过回归的方法，将x0x_0x0回归到该人脸正确的形状x∗x_*x∗上，用数学的方式表达，即为求得使下面的f(x0+Δx)f(x_0+\Delta x)f(x0+Δx)最小的Δx\Delta xΔx。
f(x0+Δx)=∣∣h(d(x0+Δx))−ϕ∗∣∣22(2)f(x_0+\Delta x)=||h(d(x_0+\Delta x))-\phi_*||_2^2\tag{2}f(x0+Δx)=∣∣h(d(x0+Δx))−ϕ∗∣∣22(2)
其中ϕ∗=h(d(x∗))\phi_*=h(d(x_*))ϕ∗=h(d(x∗))表示该人脸的真实特征点所提取出的SIFT特征，当然，上面说的是在预测时我们的目标，在预测时我们只有初始的x0x_0x0,而Δx\Delta xΔx和ϕ∗\phi_*ϕ∗我们是不知道的。在训练时，我们是知道Δx\Delta xΔx和ϕ∗\phi_*ϕ∗的，我们要在训练时训练得到一个良好的回归器，使它能够让初始的x0x_0x0一步步回归到正确的未知的形状上去。一般来说初始的x0x_0x0就是所有已知样本的真实形状的平均形状。示意图如下图所示。

那么问题来了，如果每一张脸的初始形状都是一样的（即都是已知样本的真实形状的平均形状），那么怎么让它们回归到各自人脸的真实形状呢，答案就是每张图片提取出的不同的SIFT特征（具体采用什么特征可以依据情况而定，论文中采用了SIFT特征，但也可以采用如HOG，DOG，甚至LBF等特征）了，虽然采用了相同的初始形状，但在不同的图片上，相同的初始形状所提取出的SIFT特征是完全不同的，也就是ϕ0\phi_0ϕ0是不同的，这样就可以通过回归器将其回归到各自的真实形状上了。这一点通过上面的公式也能看出。

现在我们已经有了优化的目标，就是要得到一个回归器，这个回归器能起到的作用是将一个初始形状回归到真实形状上去。也就是学到正确的回归器使其得到最好的Δx\Delta xΔx 。当然想要从初始形状一步步回归到真实形状，只学习一个Δx\Delta xΔx一般是不行的，因为一步就回归到最小点一般来说要求比较高，即使是牛顿步回归的比较快，通常也不能一步就达到目标。所以我们要学习得到多个不同的回归器，它们依次回归下来，能得到一系列的Δx\Delta xΔx,这样我们就能很快根据xk+1=xk+Δxx_{k+1}=x_k+\Delta xxk+1=xk+Δx得到使目标函数最小的点。

下面从牛顿步开始引出SDM。
首先再写一遍目标函数，如下：
f(x0+Δx)=∣∣h(d(x0+Δx))−ϕ∗∣∣22(3)f(x_0+\Delta x)=||h(d(x_0+\Delta x))-\phi_*||_2^2\tag{3}f(x0+Δx)=∣∣h(d(x0+Δx))−ϕ∗∣∣22(3)
我们使用的是从初始特征点周围提取的SIFT特征作为第一次回归的输入，然而SIFT算子是不可导的，所以如果想要使用一阶或者二阶方法来最小化上面的目标函数，那就只能用数值逼近的方法来估计Jacobian和Hessian矩阵（比如有限差分方法等）。然而数值估计计算量非常大，所以我们要采用SDM方法来学习下降的方向和下降的尺度，或者说学习Jaobian和Hessian矩阵。

为了从牛顿步开始引出SDM，我们首先假设h()h()h()这个SIFT特征提取函数是二次可导的。这样才能计算Hessian矩阵。

以下部分推导和论文不同，论文中只给了结论，我补充了论文没有写的推导过程。同时优化了一下牛顿步的推导过程。

第一步，我们首先获得一个初始的形状x0x_0x0,采用的方式是用所有训练样本的真实形状的平均形状给x0x_0x0赋值，也就是说我们迭代的初值为:
KaTeX parse error: \tag works only in display equations
接着就可以根据公式（3）计算f(x0)f(x_0)f(x0)，即令Δx=0\Delta x=0Δx=0。

现在我们已经有了f(x0)f(x_0)f(x0),我们想要知道朝什么样的方向改变x0x_0x0并且改变多少x0x_0x0可以得到一个好的f(x1)f(x_1)f(x1)，使f(x1)f(x_1)f(x1)尽量接近全局最小值，这里f(x1)f(x_1)f(x1)=f(x0+Δx)f(x_0+\Delta x)f(x0+Δx)。

我们在x0x_0x0点对f(x)f(x)f(x)进行二阶泰勒展开，如下：
f(x)=f(x0)+Jf(x0)T(x−x0)+12(x−x0)TH(x0)(x−x0)+o(∣x−x0∣2)(5)f(x)=f(x_0)+J_f(x_0)^T(x-x_0)+\frac12(x-x_0)^TH(x_0)(x-x_0)+o(|x-x_0|^2)\tag{5}f(x)=f(x0)+Jf(x0)T(x−x0)+21(x−x0)TH(x0)(x−x0)+o(∣x−x0∣2)(5)
等式最右边一项是高阶项，可以忽略。也就是说，我们要优化的目标，就是下面这个二次型，我们要极小化下面的二次型：
f(x)=f(x0)+Jf(x0)T(x−x0)+12(x−x0)TH(x0)(x−x0)(6)f(x)=f(x_0)+J_f(x_0)^T(x-x_0)+\frac12(x-x_0)^TH(x_0)(x-x_0)\tag{6}f(x)=f(x0)+Jf(x0)T(x−x0)+21(x−x0)TH(x0)(x−x0)(6)
因为要极小化f(x)f(x)f(x)，所以我们要对xxx进行求导，并且令导数等于0，以此来求出优化的方向和大小，下面对每一项进行求导：
df(x)dx=∇f(x)(7)\frac{d f(x)}{d x}=\nabla f(x)\tag{7}dxdf(x)=∇f(x)(7)
df(x0)dx=0(8)\frac{d f(x_0)}{d x}=0\tag{8}dxdf(x0)=0(8)
dJf(x0)T(x−x0)dx=Jf(x0)(9)\frac{d J_f(x_0)^T(x-x_0)}{d x}=J_f(x_0)\tag{9}dxdJf(x0)T(x−x0)=Jf(x0)(9)
d12(x−x0)TH(x0)(x−x0)dx=12[H(x0)+H(x0)T](x−x0)=H(x0)(x−x0)(10)\frac{d \frac12(x-x_0)^TH(x_0)(x-x_0)}{d x}=\frac12[H(x_0)+H(x_0)^T](x-x_0)=H(x_0)(x-x_0)\tag{10}dxd21(x−x0)TH(x0)(x−x0)=21[H(x0)+H(x0)T](x−x0)=H(x0)(x−x0)(10)
因此，求导后得到：
∇f(x)=0+Jf(x0)+H(x0)(x−x0)(11)\nabla f(x)=0+J_f(x_0)+H(x_0)(x-x_0)\tag{11}∇f(x)=0+Jf(x0)+H(x0)(x−x0)(11)
令导数等于0，得：
∇f(x)=Jf(x0)+H(x0)(x−x0)=0(12)\nabla f(x)=J_f(x_0)+H(x_0)(x-x_0) = 0\tag{12}∇f(x)=Jf(x0)+H(x0)(x−x0)=0(12)
可以解得：
x=x0−H−1(x0)Jf(x0)(13)x=x_0-H^{-1}(x_0)J_f(x_0)\tag{13}x=x0−H−1(x0)Jf(x0)(13)
即
x1=x0−H−1(x0)Jf(x0)(14)x_1=x_0-H^{-1}(x_0)J_f(x_0)\tag{14}x1=x0−H−1(x0)Jf(x0)(14)
这即得到牛顿步的表达式。
我们的第一次迭代的步长用牛顿步的方法求解就是：
Δx1=−H−1(x0)Jf(x0)(15)\Delta x_1=-H^{-1}(x_0)J_f(x_0)\tag{15}Δx1=−H−1(x0)Jf(x0)(15)
如果在目标函数二次可导的情况下，一直使用牛顿步计算出Δx2\Delta x_2Δx2、Δx3\Delta x_3Δx3、…、Δxk\Delta x_kΔxk，那么可以根据更新表达式（如下）一直计算得到新的xxx，直到得到最优解。
xk+1=xk+Δxk(16)x_{k+1}=x_k+\Delta x_k\tag{16}xk+1=xk+Δxk(16)
不过使用牛顿步计算几个Δx\Delta xΔx就要算几次Jacobian和Hessian矩阵，计算量之大可想而知了，况且目标函数还不一定二次可导（之前的二次可导是我们假设的，现在我们将去掉二次可导这个约束条件）。

下面开始推导得到我们要的SDM的方法，是接着上面牛顿步的推导而来的：

首先引入矩阵的链式求导法则如下：
df(g(x))dx=dgT(x)dxdf(g)dg(17)\frac{df(g(x))}{dx}=\frac{dg^T(x)}{dx}\frac{df(g)}{dg}\tag{17}dxdf(g(x))=dxdgT(x)dgdf(g)(17)
应用矩阵的链式求导法则：
Jf(x0)=df(x)dx∣x=x0=d∣∣h(d(x))−ϕ∗∣∣22dx∣x=x0=d(ϕx−ϕ∗)Tdx∣x=x0⋅d∣∣ϕx−ϕ∗∣∣22d(ϕx−ϕ∗)∣x=x0J_f(x_0)=\frac{d f(x)}{d x}|_{x=x_0}=\frac{d||h(d(x))-\phi_*||^2_2}{dx}|_{x=x_0}=\frac{d(\phi_x-\phi_*)^T}{dx}|_{x=x_0}\cdot\frac{d||\phi_x-\phi_*||^2_2}{d(\phi_x-\phi_*)}|_{x=x_0}Jf(x0)=dxdf(x)∣x=x0=dxd∣∣h(d(x))−ϕ∗∣∣22∣x=x0=dxd(ϕx−ϕ∗)T∣x=x0⋅d(ϕx−ϕ∗)d∣∣ϕx−ϕ∗∣∣22∣x=x0
(18)\tag{18}(18)
其中：
d(ϕx−ϕ∗)Tdx∣x=x0=dϕxTdx∣x=x0=dhT(d(x))dx∣x=x0=JhT(x0)(19)\frac{d(\phi_x-\phi_*)^T}{dx}|_{x=x_0}=\frac{d\phi_x^T}{dx}|_{x=x_0}=\frac{dh^T(d(x))}{dx}|_{x=x_0}=J_h^T(x_0)\tag{19}dxd(ϕx−ϕ∗)T∣x=x0=dxdϕxT∣x=x0=dxdhT(d(x))∣x=x0=JhT(x0)(19)
d∣∣ϕx−ϕ∗∣∣22d(ϕx−ϕ∗)∣x=x0=d[(ϕx−ϕ∗)T(ϕx−ϕ∗)]d(ϕx−ϕ∗)∣x=x0=2(ϕx−ϕ∗)∣x=x0=2(ϕ0−ϕ∗)(20)\frac{d||\phi_x-\phi_*||_2^2}{d(\phi_x-\phi_*)}|_{x=x_0}=\frac{d[(\phi_x-\phi_*)^T(\phi_x-\phi_*)]}{d(\phi_x-\phi_*)}|_{x=x_0}=2(\phi_x-\phi_*)|_{x=x_0}=2(\phi_0-\phi_*)\tag{20}d(ϕx−ϕ∗)d∣∣ϕx−ϕ∗∣∣22∣x=x0=d(ϕx−ϕ∗)d[(ϕx−ϕ∗)T(ϕx−ϕ∗)]∣x=x0=2(ϕx−ϕ∗)∣x=x0=2(ϕ0−ϕ∗)(20)
所以：
Jf(x0)=2JhT(x0)(ϕ0−ϕ∗)(21)J_f(x_0)=2J^T_h(x_0)(\phi_0-\phi_*)\tag{21}Jf(x0)=2JhT(x0)(ϕ0−ϕ∗)(21)
因此
x=x0−H−1(x0)Jf(x0)=x0−2H−1(x0)JhT(x0)(ϕ0−ϕ∗)(22)x=x_0-H^{-1}(x_0)J_f(x_0)=x_0-2H^{-1}(x_0)J^T_h(x_0)(\phi_0-\phi_*)\tag{22}x=x0−H−1(x0)Jf(x0)=x0−2H−1(x0)JhT(x0)(ϕ0−ϕ∗)(22)
所以我们的SDM方法的Δx1\Delta x_1Δx1为：
Δx1=−2H−1(x0)JhT(x0)(ϕ0−ϕ∗)(23)\Delta x_1=-2H^{-1}(x_0)J^T_h(x_0)(\phi_0-\phi_*)\tag{23}Δx1=−2H−1(x0)JhT(x0)(ϕ0−ϕ∗)(23)
看起来好像和牛顿步的Δx1=−H−1(x0)Jf(x0)\Delta x_1=-H^{-1}(x_0)J_f(x_0)Δx1=−H−1(x0)Jf(x0)区别不大，然而接下来就会看到区别：
Δx1=−2H−1(x0)JhT(x0)(ϕ0−ϕ∗)=Δx1=−2H−1(x0)JhT(x0)ϕ0+2H−1(x0)JhT(x0)ϕ∗\Delta x_1=-2H^{-1}(x_0)J^T_h(x_0)(\phi_0-\phi_*)=\Delta x_1=-2H^{-1}(x_0)J^T_h(x_0)\phi_0+2H^{-1}(x_0)J^T_h(x_0)\phi_*Δx1=−2H−1(x0)JhT(x0)(ϕ0−ϕ∗)=Δx1=−2H−1(x0)JhT(x0)ϕ0+2H−1(x0)JhT(x0)ϕ∗
(24)\tag{24}(24)
设R0=−2H−1(x0)JhT(x0)R_0=-2H^{-1}(x_0)J^T_h(x_0)R0=−2H−1(x0)JhT(x0)，b0=2H−1(x0)JhT(x0)ϕ∗b_0=2H^{-1}(x_0)J^T_h(x_0)\phi_*b0=2H−1(x0)JhT(x0)ϕ∗,可将上式表示成:
Δx1=R0ϕ0+b0(25)\Delta x_1=R_0\phi_0+b_0\tag{25}Δx1=R0ϕ0+b0(25)
也就是说，第一次增量Δx1\Delta x_1Δx1变成了特征ϕ0\phi_0ϕ0的一次函数，而我们只需要知道R0R_0R0和b0b_0b0就可以直接算出第一次的增量Δx1\Delta x_1Δx1！！！
也许有人会问，但是根据你前面的公式，你的R0R_0R0和b0b_0b0也是在计算Jacobian和Hessian矩阵的基础上计算出来的啊，说的没错，但既然现在已经将目标Δx1\Delta x_1Δx1写成了ϕ0\phi_0ϕ0的一次函数，我们计算的R0R_0R0和b0b_0b0难道还要绕回去算Jacobian和Hessian矩阵么，当然不可能了，我们只需要用我们最常用的方法，最小二乘即可！！
即最小化下面这个目标函数：
loss=∣∣Δx1−R0ϕ0−b0∣∣22(26)loss=||\Delta x_1-R_0\phi_0-b_0||_2^2\tag{26}loss=∣∣Δx1−R0ϕ0−b0∣∣22(26)
此时可以由最小二乘的公式直接得到R0R_0R0和b0b_0b0，这里就不写了。
得到了R0R_0R0和b0b_0b0,也就可以依法得到R1R_1R1、b1b_1b1、…、RkR_kRk和bkb_kbk，也就可以算出对应的的Δx2\Delta x_2Δx2、…、Δxk+1\Delta x_{k+1}Δxk+1，这些Δx\Delta xΔx就是我们要的每一次的xxx的变化方向和变化的尺度，也是根据更新公式更新，直到得到最小点的xxx。

有了R1R_1R1、b1b_1b1、…、RkR_kRk和bkb_kbk，在测试样本进行回归的时候，就可以直接进行回归。

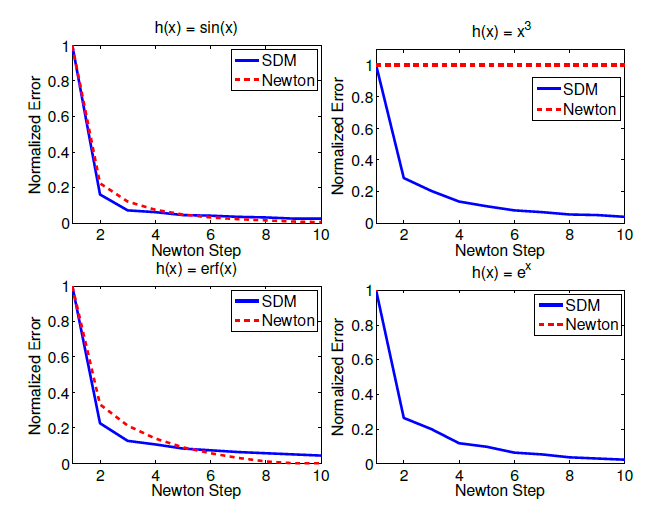
下图是作者做的对比试验（控制的变量是特征提取函数h()h()h()不同）：
有图可见，SDM的收敛速度比牛顿步更快，只是收敛得最终结果并没有达到最优（比牛顿步差一点），但SDM更具鲁棒性，在函数的Hessian矩阵不是正定的时候，SDM也能很快收敛。

做个总结：
SDM方法在更新xxx时，就是将更新的增量Δx\Delta xΔx的计算方法进行了改变，由牛顿步的计算Jacobian和Hessian矩阵来得到增量Δx\Delta xΔx，变成了计算RkR_kRk和bkb_kbk来得到增量Δx\Delta xΔx,通过推导将每一次的增量Δx\Delta xΔx变成了该次输入的特征ϕ\phiϕ的一次函数，并通过最小二乘直接计算一次函数的系数RkR_kRk和bkb_kbk，大大减少了计算量。