3.3　积性函数的实验范例

首先，我们必须弄清楚什么是积性函数：
在非数论领域，积性函数是指所有对于任何a和b都有性质f(ab)=f(a)f(b)的函数。 在数论领域，考虑一个函数值为正整数的函数f，对于任意两个互质的正整数a和b，均满足f(ab)=f(a)f(b)，则函数f称为积性函数。假如对于任意两个正整数a和b，都有f(ab)=f(a)f(b)，则函数f也称为完全积性函数。 容易看出，对于任意积性函数（包括完全积性函数），f(1)=1。
由于任何一个大于1的自然数N都可以唯一分解成有限个质数的乘积，因此积性函数f(N)的值完全由质数的幂决定。也就是说，若将N表示成质因子分解式N=Πpaii，其中pi为互不相同的质数，那么对于一个积性函数f，f(N)=f(Πpaii)=Π f(paii)。如果f还满足完全积性，则f(N)= Π f ai(pi)。
下面介绍数论中两个常见的积性函数：
1)欧拉函数φ(n)，用于计算与n互质的正整数个数。
2)莫比乌斯函数μ(n)，用于计算非平方数n的质因子个数，μ(n)为φ(n)的反演函数。
3.3.1　使用欧拉函数φ(n)计算与n互质的正整数个数
欧拉函数φ(n)表示{1，…，n}中与n互质的整数个数。例如，φ(1)=φ(2)=1，φ(3)=φ(4)=2。
当n是素数时，φ(n)=n-1。
当n是合数时，φ(n)若m、n互质，φ(mn)=φ(m)φ(n)。
显然，φ(n)为积性函数，但不是完全积性函数。
考虑一个质数p和正整数k，不难看出φ(pk)=pk-pk-1=(p-1)pk-1。
在数论中，欧拉定理具有一个关于同余的性质。
欧拉定理：若n和a为正整数且n和a互质（gcd(a，n)=1），则aφ(n)≡1 (mod n)。
证明：
首先证明下面这个命题：
对于集合Zn={x1,x2,...,xφ(n)},其中xi是不大于n且与n互素的数(1≤i≤φ(n))，即n的一个化简剩余系(或称简系，或称缩系)。考虑集合S={ ax1(mod n),ax2(mod n),...,a*xφ(n)(mod n)}，则S=Zn。
证明：
1)由于a、n互质，xi也与n互质，则axi也一定与n互质，因此对于任意xi，axi(mod n) 必然是Zn的一个元素。
2)对于Zn中两个元素xi和xj，如果xi≠xj，则axi(mod n) ≠ axj(mod n)，这个由a、n互质和消去律可以得出。
所以，很明显，S=Zn。
既然这样，那么 （ax1ax2…axφ(n)）(mod n)
=(［aφ(n)］x1x2…xφ(n))(mod n)
=（(ax1(mod n))(ax2(mod n))…(axφ(n)(mod n))）(mod n)
=（x1x2…xφ(n)）(mod n) 　　考虑等式 (［aφ(n)］x1x2…xφ(n))(mod n)=（x1x2…xφ(n)）(mod n)。由于x1x2…*xφ(n)与n互质，因此根据消去律可从等式两边约去，于是得到欧拉定理aφ(n)≡1(mod n)。
推论：对于互质的数a、n，满足aφ(n)+1≡a(mod n) 。
欧拉定理的一个特例是费马定理。
费马定理：假如p是质数且a与p互质，则 ap-1 ≡1(mod p)。另一种形式是，设p是素数, 则对任意的整数a，ap≡a(mod p)。
证明费马定理非常简单，只要将φ(p)=p-1代入欧拉定理aφ(n)≡1(mod n)即可证明。在a能被p整除时，ap≡a(mod p)的结论显然成立。费马定理提供了一种不用因子分解就能断定一个数是合数的新途径。例如29-1≡4(mod 9),可以断定9是合数。
欧拉函数有两个重要性质：
性质1：∑dnφ(d)=n。
性质2：当n>1时， 1…n中与n互质的整数和为nφ(n)2。
下面给出欧拉函数的程序示例：

bool u［1111111］;// 筛子
int su［1111111］,num=1； // 素数表。表长为num
int f［1111111］// 欧拉函数
int i,j,
f［1］=1;// 设置1的欧拉函数值
memset(u,true,sizeof(u));
for(i=2;i<=n;i++){// 顺序分析整数区间的每个数
if(u［i］)// 将筛中最小数送入素数表，并计算其欧拉函数值{ su［num++］=i; f［i］=i-1 } ；
for(j=1;j<num;j++) {// 搜索素数表的每个数if (i*su［j］>n) break;　　u［i*su［j］］=false;// 将i与当前素数的乘积从筛子中筛去if (i% su［j］)// 根据当前素数是否为i的素因子，分情形计算欧拉函数{ f［i*su［j］］=f［i］*(su［j］-1)}else { f［i*su［j］］=f［i］*su［j］ ; break; }
}
}

欧拉函数可应用于许多具有积性性质的数论问题。例如:
1)设对质数p取模意义下n的乘法逆元为f(n)，现在要求出f(1)、f(2)、…、f(n)。
解法：很容易看出f是完全积性函数，这样如果对于质数p求出了f(p)的值，任意f(n)就能求出了。因此可采用线性筛法求逆元。用扩展欧几里得算法求一次乘法逆元的时间复杂度为O(log2n)，而质数的个数正好为nlog2n，因此这个算法的时间复杂度为O(n)。其实这个问题并没有这么麻烦。设p=nt+k，则f(n)=(nt2*f(k)2)mod p。
证明过程如下：∵nt≡-k(mod p)→ntf(k)≡-1(mod p)→n2t2f(k)2≡1(mod p)
∴n-1≡nt2f(k)2(mod p)显然，由于1≤k2)求c(n，m)mod P，其中0≤m≤n≤106，P为大质数。
解法：根据c(n，m)=n!m!(n-m)!，可以用时效为O(m*log2m)的“蛮力算法”求解。其实这题可以利用预处理（预先计算n!-1）加速计算。由逆元的积性，可得n!-1≡∏nk=1k!－1≡∏nk=1f(k)%p这样也就能线性预处理阶乘的逆元了。这个算法能在某些组合计数问题中派上用场。
由于欧拉函数的程序基本上是模式化的，因此解题的关键是如何将数论问题抽象成计算与n同质的正整数个数的数学模型。只要能够抽象出相应的数学模型，程序编写就变得轻而易举了。
【3.3.1.1　Relatives】
【问题描述】
给出一个正整数n，有多少个小于n的正整数是对于n的相对素数？如果不存在整数x>1、y>0、z>0使得a=xy，且b=xz，则两个整数a和b是相对素数。
输入：
给出若干测试用例。每个测试用例占一行，给出n≤1000000000。在最后一个测试用例后的一行给出0。
输出：
对每个测试用例输出一行，给出上述问题的答案。

试题来源：Waterloo local 2002.07.01
在线测试地址：POJ 2407，ZOJ 1906，UVA 10299
试题解析
n的相对素数的个数为欧拉函数φ(n)，这个函数为积性函数，即n若分解出k个素数乘幂形式n=pe11 pe22…pekk，则φ(n)=φ(p1)φ(p2)…φ(pk)其中φ(pi)=(pi-1)pei-1i（1≤i≤k）程序清单

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdio>
#include<cstdlib>using namespace std;typedef long long ll;
bool u［50000］;// 素数筛
ll su［50000］,num;// 长度为num的素数表ll gcd(ll a,ll b){// 计算a和b的最大公约数if(b==0)return a;return gcd(b,a%b);
}void prepare(){// 使用筛选法构建［2..50000］内的素数表su［］
ll i,j,num;memset(u,true,sizeof(u));for(i=2;i<= 50000;i++){// 顺序分析整数区间的每个数if(u［i］) su［++num］=i;// 将筛中最小数送入素数表for(j=1;j<=num;j++) {// 搜索素数表的每个数if (i*su［j］>n)break;　　u［i*su［j］］=false;// 将i与当前素数的乘积从筛子中筛去if (i% su［j］==0) break;// 若当前素数为i的素因子，则分析下一个整数}
}
}ll phi(ll x)// 计算x的欧拉函数φ(x)，即若x分解出k个素因子
// p1、p2、…、pk，则对于x的相对素数的个数φ(x)=
// φ(p1)*φ(p2)*…*φ(pk)
{ll ans=1;//  设置φ(x)的初值int i,j,k;for(i=1;i<=num;i++)if(x%su［i］==0){// 若x含素因子su［i］，则计算其次幂j。φ(su［i］)=
//  (su［i］-1)*su［i］j-1乘入φ(x)j=0;while(x%su［i］==0){++j;x/=su［i］;}for(k=1;k<j;k++)ans=ans*su［i］%1000000007ll;ans=ans*(su［i］-1)%1000000007ll;if(x==1)break;}if(x>1)ans=ans*(x-1)%1000000007ll;// 最后的φ(pk)=pk-1乘入φ(x)return ans;// 返回φ(x)
}int main(){prepare();// 使用筛选法构建［2.. 50000］内的素数表su［］int n,i,j,k;ll ans=1;while(scanf("%d",&n)==1&&n>0){// 反复输入整数n，直至输入0为止ans=phi(n);// 计算和输出φ(n)printf("%d＼n",(int)ans);}
}

【3.3.1.2　Primitive Roots】
【问题描述】
我们称整数x(0请编写一个程序，给出任何一个奇素数3≤p<65536，输出p为模的本原根的数目。
输入：
每行输入给出一个奇素数p，输入以EOF结束。
输出：
对每个p，输出一行，给出一个整数，给出本原根的数目。

试题来源：贾怡@pku
在线测试地址：POJ 1284
试题解析
由本原根的定义可以看出，整数x（0令g为本原根，当且仅当gi能遍历n的缩剩余系（与n互素的剩余系），n的缩剩余系与乘法运算构成了一个φ(n)阶的循环群。
假设现有一个n阶的循环群，g为这个群的一个生成元。若gk也为此群的生成元，则有(gk)m=g1 ，k*m≡1(mod n)，即m的方程有解当且仅当gcd(k，n)=1。显然，n阶的循环群的生成元共有φ(n)个。由此得到结论：
若n存在本原根，则其共有φ(φ(n))个本原根。由于题目中p为素数，p一定存在本原根，且φ(p)=p-1，所以答案就是φ(p-1)。
程序清单

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdio>
#include<cstdlib>using namespace std;typedef long long ll;
bool u［50000］;　　　　　　　　　　　　　　　　// 素数筛
ll su［50000］,num;// 长度为num的素数表void prepare(){// 采用筛选法计算素数表su［］ll i,j,k;for(i=2;i<50000;i++)u［i］=1;for(i=2;i<50000;i++)if(u［i］)for(j=2;j*i<50000;j++) u［i*j］=0;for(i=2;i<50000;i++)if(u［i］) su［++num］=i;
}ll phi(ll x)// 计算欧拉函数φ(x)，即若x分解出k个素因子p1，p2，…，pk，
// 则φ(x)=φ(p1)*φ(p2)*…*φ(pk)%1000000007
{ll ans=1;int i,j,k;for(i=1;i<=num;i++)// 按照递增顺序枚举每个素数if(x%su［i］==0){// 若x含次幂为j的素因子su［i］，则计算φ(s［i］)=
// su［i］j-1*(su［i］-1)，并乘入φ(x)j=0;while(x%su［i］==0){++j;x/=su［i］;}for(k=1;k<j;k++)ans=ans*su［i］%1000000007ll;ans=ans*(su［i］-1)%1000000007ll;if(x==1)break;}if(x>1)ans=ans*(x-1)%1000000007ll;// 最后一项乘入φ(x)return ans;
}int main(){prepare();// 采用筛选法计算素数表su［］int n,i,j,k;ll ans=1;while(scanf("%d",&n)==1){// 反复输入模n，直至输入EOF为止ans=phi(n-1);// 计算和输出以n为模的本原根的数目printf("%d＼n",(int)ans);}
}

3.3.2　使用莫比乌斯函数μ(n)计算非平方数n的质因子个数
若f(n)为积性函数，则函数g(n)= ∑dnf(d)也是积性函数。根据积性函数的性质，函数h(n)=f(n)g(n)为积性函数，反之亦然。由此得出莫比乌斯反演公式：f(n)= ∑dnμ(d)g(nd)其中μ是一个定义域为N的积性函数：
μ(1)=1。
当n存在平方因子时，μ(n)=0。
当n是素数或奇数个不同素数之积时，μ(n)=-1。
当n是偶数个不同素数之积时，μ(n)=1。
图3.3-1给出了μ(n)的前50个值：1,-1,-1, 0,-1,1,-1, 0, 0, 1,-1, 0,-1, 1, 1, 0,-1, 0,-1, 0, 1, 1,-1, 0, 0,…。

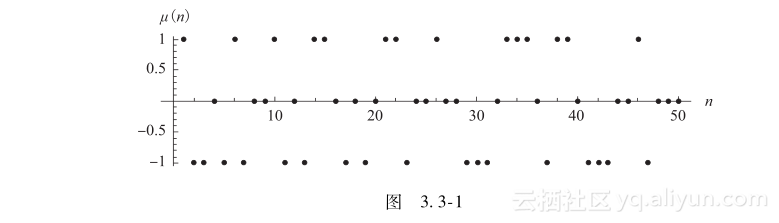
由此得出∑dnμ(n)=1n=1
0其他状况下面给出莫比乌斯函数的程序示例：

bool u［1111111］;　　　　　　　　　　　　// 筛子
int su［1111111］,num=1；// 素数表。表长为num
int mu［1111111］// 莫比乌斯函数
int i,j,mu［1］=1;// 设置1的莫比乌斯函数值
memset(u,true,sizeof(u));
for(i=2;i<=n;i++){// 顺序分析整数区间的每个数if(u［i］)// 将筛中最小数送入素数表，并设置其莫比乌斯函数值{ su［num++］=i; mu［i］=-1 } ；for(j=1;j<num;j++) {// 搜索素数表的每个数if (i*su［j］>n) break;u［i*su［j］］=false;// 将i与当前素数的乘积从筛子中筛去if (i% su［j］)// 根据当前素数是否为i的素因子，分情形计算莫比乌斯函数值{ mu［i*su［j］］=-mu［i］;}else { mu［i*su［j］］=0; break }}
}

利用莫比乌斯反演可以求得欧拉函数。设f(n)=∑dnφ(d)。根据欧拉函数性质可知f(n)=n，又有φ(n)= ∑dnμ(d)f(nd)，因此φ(n)= ∑dnμ(d)nd。
莫比乌斯反演利用的是偏序集上的容斥原理。我们从另一个角度来理解一下上述公式：考虑不超过n的正整数k，根据欧拉函数的定义，我们要算出有多少k与n互质。
令gcd(n，k)=d，当d>1要被去除，考虑质数集合P={2,3,5,7,11,13…}，d>1时显然会是P中某些质数的倍数。若p|d，可知满足这样条件的k有np个。这些是需要去掉的，但很容易发现中间有重复；继续考虑两个不同质数p1、p2，若p1p2|d，则这样的d被重复去掉两次，需要加上np1p2；接着考虑三个不同质数p1、p2、p3，若p1p2p3|d，在开始时被去掉三次，但是前面考虑两个质数时又被加回三次，因此需要再去掉np1p2p3。
依此类推，考虑t个不同的质数p1、p2、p3、…、pt，若p1p2p3…pt|d，根据容斥原理，需要加上(－1)tnp1p2p3…pt。
最后观察莫比乌斯函数定义和φ(n)= ∑dnμ(d)nd，可以发现d其实就表示若干不同质数的乘积（若不是这样的，μ(d)=0）。
求解积性函数一般采用线性筛法。积性函数的关键是如何求f(pk)。观察线性筛法中的步骤，筛掉n的同时还得到了它的最小质因数p，我们希望能够知道p在n中的次数，这样就能利用f(n)=f(pk)f(npk)求出f(n)。
令n=pm，由于p是n最小的质因数，若p2|n，则p|m，并且p也是m的最小质因数。这样在进行筛法的同时，记录每个合数最小质因数的次数，就能算出新筛去合数最小质因数的次数。但是这样还不够，我们还要能够快速求f(pk)，这时一般就要结合f函数的性质考虑。 例如欧拉函数φ，φ(pk)=(p-1)pk-1，因此进行筛法时，如果p|m，就乘上p，否则乘上p-1。再比如莫比乌斯函数μ，只有当k=1时μ(pk)=-1；否则μ(pk)=0。与欧拉函数一样，根据m是否被p整除进行判断。
【3.3.2.1　能量采集】
【问题描述】
栋栋有一块长方形的地，他在地上种了一种能量植物，这种植物可以采集太阳光的能量。在这些植物采集能量后，栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。
栋栋的植物种得非常整齐，一共有n列，每列有m棵，植物的横竖间距都一样，因此对于每一棵植物，栋栋可以用一个坐标(x, y)来表示，其中x的范围是1～n，表示是在第x列，y的范围是1～m，表示是在第x列的第y棵。
由于能量汇集机器较大，不便移动，栋栋将它放在了一个角上，坐标正好是(0, 0)。

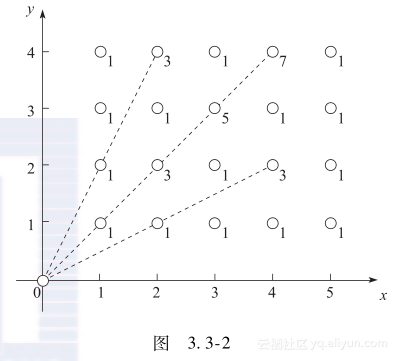
能量汇集机器在汇集的过程中有一定的能量损失。如果一棵植物与能量汇集机器连接而成的线段上有k棵植物，则能量的损失为2k+1。例如，当能量汇集机器收集坐标为(2, 4)的植物时，由于连接线段上存在一棵植物(1, 2)，则产生的能量损失为3。注意，如果一棵植物与能量汇集机器连接的线段上没有植物，则能量损失为1。现在要计算总的能量损失。
图3.3-2给出了一个能量采集的例子，其中n=5、m=4，一共有20棵植物，在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。
在这个例子中，总共产生的能量损失为36。
【输入格式】
输入文件energy.in仅包含一行，为两个整数n和m。
【输出格式】
输出文件energy.out仅包含一个整数，表示总共产生的能量损失。
【数据规模和约定】
对于10%的数据：1≤n,m≤10。
对于50%的数据：1≤n,m≤100。
对于80%的数据：1≤n,m≤1000。
对于90%的数据：1≤n,m≤10000。
对于100%的数据：1≤n,m≤100000。
【运行时限】1秒。
【运行空限】512M。

试题来源：NOI 2010
在线测试地址：BZOJ 2005　http:// www.lydsy.com/JudgeOnline/problem.php?id=2005
试题解析
试题给出了n、m，要求计算出∑nx=1∑my=1gcd(x,y)的值(n,m≤106 )。首先，我们不难看出每个点(x,y)到(0,0)的连线上共有gcd(x,y)-1个点，这样每个点对答案的贡献为2(gcd(x,y)-1)+1= 2gcd(x,y)-1。显然，最终答案为2∑nx=1∑my=1gcd(x,y)-nm。
计算的瓶颈在于如何快速算出∑nx=1∑my=1gcd(x,y)，蛮力枚举显然会超时。
令t=gcd(x,y)，换一个角度，枚举t所有可能的值，计算每个t值下有多少数对{(x，y)|x≤n，y≤m，gcd(x，y)=t}，也就是计算有多少个数对{(x，y)|x≤nt，y≤mt，gcd(x，y)=1}。令n′=nt，m′=mt，f(t)={(x,y)x≤n′,y≤m′,gcd(x,y)=tf(t)表示该范围内满足gcd(x，y)=t的数对个数。显然f(t)也不是那么容易求出的。再考虑一个函数g(t)={(x,y)x≤n′,y≤m′,gcd(x,y)=kt,k∈z+g(t)表示该范围内满足gcd(x，y)为t的倍数的数对个数。我们可以很容易得到以下结论：g(t)=n′t mt再考虑g(t)与f(t)之间的关系，显然有g(t)=∑tkf(k)。注意到g函数的值是很容易求出的，而f函数的值却非常不易求得。我们不妨对其做莫比乌斯反演f(t)=∑tkgktμ(k)。由于我们要求的是f(1)，可得f(1)=∑kg(k)*μ(k)。
这样，我们就得到了计算互质对数的公式。然而如果蛮力枚举t和k，显然也是平方级的时间复杂度，同样会超时。下面考虑如何继续优化：
首先，很容易看出nt的取值只有2n种，同理mt的取值只有2m种，并且相同取值对应的t是一个连续的区间，因此nt和mt都相同的区间最多只有2n+2m个，这样t的枚举量就缩小为O(n+m)了。如果使用线性筛法预处理μ函数的部分和，总的时间复杂度就减至O(n+m)，可见其效率非常高。
程序清单

# include <cstdio>
# include <cstring>
# include <string>
# include <algorithm>
using namespace std;
typedef long long int64;
const int N=100010;int mu［N］,smu［N］,u［N］,su［N］,num;　　　　　　　// ［2..n］的素数筛为u［］，素数表为su［］，其长度为num；
// mu［i］为μ［i］，smu［i］为μ［1］+μ［2］+…+μ［i］void cal_mu(){// 筛法计算μ函数的部分和mu［1］=smu［1］=1;// 初始化 for(int i=2;i<N;i++){ if(!u［i］)　su［num++］=i,mu［i］=-1;// 若i为素数，则i进入素数表，μ［i］=-1for(int j=0;j<num;j++){// 搜索su［］中的每个素数if((int64)i*su［j］>=N)break;// 若i与第j个素数的乘积不小于n，则退出循环；
// 否则从筛中筛去该乘积u［i*su［j］］=1;if(i%su［j］==0){// 若i能整除第j个素数，则μ［i*j个素数］=0 ，
// 退出循环；否则μ［i*j个素数］为μ［i］取反mu［i*su［j］］=0;break;}else　mu［i*su［j］］=-mu［i］;}smu［i］=smu［i-1］+mu［i］;// 计算μ函数的部分和}
}int64 getans(int n,int m){// 计算每个d下的答案int64 ans=0;for(int i=1;i<=n;i++){// 当前d值对应连续区间［i,min(n/(n/i),m/(m/i))］,计入
// 该区间的∑kg(k)*μ(k)=(∑i+lk=iμ［k］)* ni*miint l=min(n/(n/i),m/(m/i))-i;ans+=(int64)(smu［i+l］-smu［i-1］)*(n/i)*(m/i);　i+=l;// 继续计算下一连续区间}return ans;
}int main(){cal_mu();// 预处理μ函数的部分和int n,m;scanf("%d %d",&n,&m);// 输入n，mif(n>m)　swap(n,m);int64 ans=0;// 采用优化算法计算ans=∑nx=1∑my=1gcd(x,y)for(int i=1;i<=n;i++){int d=min(n/(n/i),m/(m/i)),l=d-i+1;// 相同取值对应的i为一个长度为l的连续区间［i,d］ans+=(int64(d+i)*l/2)*getans(n/i,m/i);i=d;// 继续计算下一连续区间}ans=ans*2-(int64)n*m;// 计算和输出2*∑nx=1∑my=1gcd(x,y)－n*mprintf("%lld＼n",ans);return 0;
}