一、引例：蒲丰投针实验

1、 求圆周率。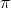

蒙特卡罗方法源于美国在第二次世界大战中研发原子弹的“曼哈顿计划”。该计划的主持人之一数学家冯·诺伊曼用驰名世界的赌城——摩纳哥的MonteCarlo来命名这种方法，其基本思想源于法国蒲丰提出著名的蒲丰投针实验，并用该办法求圆周率。

如图，在平面上画出一组平行线，他们之间的距离为，并找一根粗细均匀长度为的细针，然后将小针一次次地任意投掷在平面上。这样反复投掷多次，记录下针与这组平行线中任意一条相交的次数，就可以计算出的近似值。

蒲丰投针试验揭示了蒙特卡罗方法的基本思想：在大数定理的保证下，利用事件发生的“频率”作为事件发生的“概率”的近似值。只要设计一个随机试验，使一个事件的概率与某未知数有关，然后通过重复试验，以频率近似值表示概率，即可求得该未知数的近似值。显然利用随机试验求近似解，试验次数要相当多才行，且次数越多近似效果也越好。此种方法可以求解微分方程，求多重积分，求特征值等。

2、Matlab模拟投针实验

%%【1】代码部分
l =  0.520;     % 针的长度（任意给的）
a = 1.314;    % 平行线的宽度(大于针的长度l即可)
n = 1000000;    % 做n次投针试验，n越大求出来的pi越准确
m = 0;    % 记录针与平行线相交的次数
x = rand(1, n) * a / 2 ;   % 在[0, a/2]内服从均匀分布随机产生n个数， x中每一个元素表示针的中点和最近的一条平行线的距离
phi = rand(1, n) * pi;    % 在[0, pi]内服从均匀分布随机产生n个数，phi中的每一个元素表示针和最近的一条平行线的夹角
% axis([0,pi, 0,a/2]);   box on;  % 画一个坐标轴的框架，x轴位于0-pi，y轴位于0-a/2， 并打开图形的边框
for i=1:n  % 开始循环，依次看每根针是否和直线相交if x(i) <= l / 2 * sin(phi (i))     % 如果针和平行线相交m = m + 1;    % 那么m就要加1
%         plot(phi(i), x(i), 'r.')   % 模仿书上的那个图，横坐标为phi，纵坐标为x , 用红色的小点进行标记
%         hold on  % 在原来的图形上继续绘制end
end
p = m / n;    % 针和平行线相交出现的频率
mypi = (2 * l) / (a * p);  % 我们根据公式计算得到的pi
disp(['蒙特卡罗方法得到pi为：', num2str(mypi)])

得到的结果如图，结果为3.368。

因为随机数是由计算机产生的，因此每一次输出的结果都可能相同，并且n的值越大，结果越接近真实值，为了提高准确性，我们可以利用MATLAB的for循环模拟100次（或者更多次），最后求平均值得到结果。

result = zeros(100,1);  % 初始化保存100次结果的矩阵
l =  0.520;     a = 1.314;
n = 1000000;
for num = 1:100m = 0;  x = rand(1, n) * a / 2 ;phi = rand(1, n) * pi;for i=1:nif x(i) <= l / 2 * sin(phi (i))m = m + 1;endendp = m / n;mypi = (2 * l) / (a * p);result(num) = mypi;  % 把求出来的myphi保存到结果矩阵中
end
mymeanpi = mean(result);  % 计算result矩阵中保存的100次结果的均值
disp(['蒙特卡罗方法得到pi为：', num2str(mymeanpi)])

现在输出的值更接近值。

二、蒙特卡罗方法概述

1、步骤

1. 人为地描述或者构造概率过程。
2. 通过计算机产生已知概率分布的随机变量，常用的概率分布有均匀分布，正态分布，指数分布，泊松分布等。[重点步骤，当不知道随机变量的概率模型服从那个分布时，可以使用均匀分布来构造；各种测量的误差、射击命中率、人的身高与体重等服从正态分布；指数分布可用在排队论与可靠性分析中；泊松分布可用在产品检验、排队系统、物理等领域中]
3. 建立各种估计量。

2、讨论

3、已经举过的例子

三、蒙特卡罗方法在数学建模中的应用举例

1、三门问题：

你参加一档电视节目，节目组提供了ABC三扇门,主持人告诉你，其中一扇门后边有辆汽车，其它两扇门后是空的。假如你选择了B门，这时，主持人打开了C门，让你看到C门后什么都没有，然后问你要不要改选A门?

代码预备知识：a.字符串连接方式|b.num2str函数

%% （1）预备知识
% randi([a,b],m,n)函数可在指定区间[a,b]内随机取出大小为m*n的整数矩阵
randi([1,5],5,8) %在区间[1,5]内随机取出大小为5*8的整数矩阵
%      2     5     4     5     3     1     4     2
%      3     3     1     5     4     2     1     2
%      4     1     3     3     2     2     5     1
%      5     3     3     4     4     5     4     4
%      4     2     3     4     2     4     2     4
randi([1,5])   %在区间[1,5]内随机取出1个整数
%     3% 字符串的连接方式：(1)['字符串1','字符串2'] (2)strcat('字符串1','字符串2') （第一期视频第一讲）
['数学建模','学习交流']
strcat('数学建模','学习交流')% num2str函数：将数值转换为字符串 （第一期视频第一讲）
mystr = num2str(1224)  % 注意观察工作区的mystr这个变量的值
disp([num2str(1224),'祝大家平安夜平平安安'])  % disp函数是输出函数

模拟三门问题代码

%%  蒙特卡罗用于模拟三门问题
clear;clc%% 代码部分（在成功的条件下的概率）
n = 100000;  % n代表蒙特卡罗模拟重复次数
a = 0;  % a表示不改变主意时能赢得汽车的次数
b = 0;  % b表示改变主意时能赢得汽车的次数
for i= 1 : n  % 开始模拟n次x = randi([1,3]);  % 随机生成一个1-3之间的整数x表示汽车出现在第x扇门后y = randi([1,3]);  % 随机生成一个1-3之间的整数y表示自己选的门% 下面分为两种情况讨论：x=y和x~=yif x == y   % 如果x和y相同，那么我们只有不改变主意时才能赢a = a + 1;     b = b + 0;else  % x ~= y ，如果x和y不同，那么我们只有改变主意时才能赢a = a + 0;     b = b +1;end
end
disp(['蒙特卡罗方法得到的不改变主意时的获奖概率为：', num2str(a/n)]);
disp(['蒙特卡罗方法得到的改变主意时的获奖概率为：', num2str(b/n)]);%%考虑失败情况的代码(无条件概率)
n = 100000;  % n代表蒙特卡罗模拟重复次数
a = 0;  % a表示不改变主意时能赢得汽车的次数
b = 0;  % b表示改变主意时能赢得汽车的次数
c = 0;  % c表示没有获奖的次数
for i= 1 : n  % 开始模拟n次x = randi([1,3]);  % 随机生成一个1-3之间的整数x表示汽车出现在第x扇门后y = randi([1,3]);  % 随机生成一个1-3之间的整数y表示自己选的门change = randi([0, 1]); % change =0  不改变主意，change = 1 改变主意% 下面分为两种情况讨论：x=y和x~=yif x == y   % 如果x和y相同，那么我们只有不改变主意时才能赢if change == 0  % 不改变主意a = a + 1; else  % 改变了主意c= c+1;endelse  % x ~= y ，如果x和y不同，那么我们只有改变主意时才能赢if change == 0  % 不改变主意c = c + 1; else  % 改变了主意b= b + 1;endend
end
disp(['蒙特卡罗方法得到的不改变主意时的获奖概率为：', num2str(a/n)]);
disp(['蒙特卡罗方法得到的改变主意时的获奖概率为：', num2str(b/n)]);
disp(['蒙特卡罗方法得到的没有获奖的概率为：', num2str(c/n)]);

2、模拟排队问题

假设某银⾏⼯作时间只有⼀个服务窗⼝，⼯作⼈员只能逐个的接待顾客。当来的顾客较多时，⼀部分顾客就需要排队等待。假设：1) 顾客到来的间隔时间服从参数为0.1的指数分布 2) 每个顾客的服务时间服从均值为10，⽅差为4的正态分布(单位为分钟，若服务时间⼩于1分钟，则按1分钟计算) 3) 排队按先到先服务的规则，且不限制队伍的⻓度，每天⼯作时⻓为8⼩时。

试回答下⾯的问题：

1) 模拟⼀个⼯作⽇，在这个⼯作⽇共接待了多少客户，客户平均等待的时间为多少?

2) 模拟100个⼯作⽇，计算出平均每⽇接待客户的个数以及每⽇客户的平均等待时⻓?

3、有约束的非线性规划问题

决策变量、目标函数和约束条件（s.t是数学规划模型的三个要素，若目标函数和约束条件均为线性的数学规划问题称为线性规划，否则称为非线性规划。

%%  蒙特卡罗求解有约束的非线性规划问题
% max f(x) = x1*x2*x3
% s.t.
% (1) -x1+2*x2+2*x3>=0
% (2) x1+2*x2+2*x3<=72
% (3) x2<=20 & x2>=10
% (4) x1-x2 == 10%% （1）预备知识
%  (1) format long g  可以将Matlab的计算结果显示为一般的长数字格式（默认会保留四位小数，或使用科学计数法）
5/7
5895*514100
format long g
5/7
5895*514100
%  (2)unifrnd(a,b,m,n)可以输出在[a,b]之间均匀分布的随机数组成的m行n列的矩阵。(等价于 a + rand(m,n)*(b-a))
unifrnd(0,5,4,3)
%           4.07361843196589          3.16179623112705          4.78753417717149
%            4.5289596853781         0.487702024997048          4.82444267599638
%           0.63493408146753          1.39249109433524         0.788065408387741
%            4.5668792806951          2.73440759602492          4.85296390880308%% （2）代码部分
clc,clear;
tic %计算tic和toc中间部分的代码的运行时间
n=10000000; %生成的随机数组数
x1=unifrnd(20,30,n,1);  % 生成在[20,30]之间均匀分布的随机数组成的n行1列的向量构成x1
x2=x1 - 10;
x3=unifrnd(-10,16,n,1);  % 生成在[-10,16]之间均匀分布的随机数组成的n行1列的向量构成x3
fmax=-inf; % 初始化函数f的最大值为负无穷（后续只要找到一个比它大的我们就对其更新）
for i=1:nx = [x1(i), x2(i), x3(i)];  %构造x向量, 这里千万别写成了：x =[x1, x2, x3]if (-x(1)+2*x(2)+2*x(3)>=0)  &  (x(1)+2*x(2)+2*x(3)<=72)     % 判断是否满足条件result = x(1)*x(2)*x(3);  % 如果满足条件就计算函数值if  result  > fmax  % 如果这个函数值大于我们之前计算出来的最大值fmax = result;  % 那么就更新这个函数值为新的最大值X = x;  % 并且将此时的x1 x2 x3保存到一个变量中endend
end
disp(strcat('蒙特卡罗模拟得到的最大值为',num2str(fmax)))
disp('最大值处x1 x2 x3的取值为：')
disp(X)
toc %计算tic和toc中间部分的代码的运行时间%% （3）缩小范围重新模拟得到更加精确的取值
clc,clear;
tic %计算tic和toc中间部分的代码的运行时间
n=10000000; %生成的随机数组数
x1=unifrnd(22,23,n,1);  % 生成在[22,23]之间均匀分布的随机数组成的n行1列的向量构成x1
x2=x1 - 10;
x3=unifrnd(11,13,n,1);  % 生成在[11,13]之间均匀分布的随机数组成的n行1列的向量构成x3
fmax=-inf; % 初始化函数f的最大值为负无穷（后续只要找到一个比它大的我们就对其更新）
for i=1:nx = [x1(i), x2(i), x3(i)];  %构造x向量, 这里千万别写成了：x =[x1, x2, x3]if (-x(1)+2*x(2)+2*x(3)>=0)  &  (x(1)+2*x(2)+2*x(3)<=72)     % 判断是否满足条件result = x(1)*x(2)*x(3);  % 如果满足条件就计算函数值if  result  > fmax  % 如果这个函数值大于我们之前计算出来的最大值fmax = result;  % 那么就更新这个函数值为新的最大值X = x;  % 并且将此时的x1 x2 x3保存到一个变量中endend
end
disp(strcat('蒙特卡罗模拟得到的最大值为',num2str(fmax)))
disp('最大值处x1 x2 x3的取值为：')
disp(X)
toc %计算tic和toc中间部分的代码的运行时间

4、书店买书问题

制定最省钱的方案

%% 书店买书问题的蒙特卡罗的模拟
%% （1）预备知识
% (1)unique函数: 剔除一个矩阵或者向量的重复值，并将结果按照从小到大的顺序排列
% adj.  唯一的; 独一无二的   [ju'ni:k]
unique([1 2 5; 6 8 9;2 4 6])
unique([5 6 8 8 4 1 6 2 2 4 8 4 5 6])% (2)randi([a,b],m,n)函数可在指定区间[a,b]内随机取出大小为m*n的整数矩阵
randi([-5,5],2,6)%% （2）代码求解
min_money = +Inf;  % 初始化最小的花费为无穷大，后续只要找到比它小的就更新
min_result = randi([1, 6],1,5);  % 初始化五本书都在哪一家书店购买，后续我们不断对其更新
%若min_result = [5 3 6 2 3]，则解释为：第1本书在第5家店买，第2本书在第3家店买，第3本书在第6家店买，第4本书在第2家店买，第5本书在第3家店买
n = 100000;  % 蒙特卡罗模拟的次数
M = [18     39 29  48  5924    45  23  54  4422    45  23  53  5328    47  17  57  4724    42  24  47  5927    48  20  55  53];  % m_ij  第j本书在第i家店的售价
freight = [10 15 15 10 10 15];  % 第i家店的运费
for k = 1:n  % 开始循环result = randi([1, 6],1,5); % 在1-6这些整数中随机抽取一个1*5的向量，表示这五本书分别在哪家书店购买index = unique(result);  % 在哪些商店购买了商品，因为我们等下要计算运费money = sum(freight(index)); % 计算买书花费的运费% 计算总花费：刚刚计算出来的运费 + 五本书的售价for i = 1:5   money = money + M(result(i),i);  endif money < min_money  % 判断刚刚随机生成的这组数据的花费是否小于最小花费，如果小于的话min_money = money  % 我们更新最小的花费min_result = result % 用这组数据更新最小花费的结果end
end
min_money   % 18+39+48+17+47+20
min_result

5、导弹追踪问题

位于坐标原点的A船向位于其正东方20个单位的B船发射导弹，导弹始终对准B船，B船以时速V单位（常数)沿东北方向逃逸。若导弹的速度为3V，导弹的射程是50个单位，画出导弹运行的曲线，导弹是否能在射程内击中B船?

%%  蒙特卡罗用于模拟导弹追击问题
% 注意，模拟导弹追击问题更像是一种仿真模拟的方法。这里本质上没有用到随机数，因此严格意义上不能称为蒙特卡罗。
clear;clc
%% （1）预备知识
% mod(m,n)表示求m/n的余数
mod(8,3)
mod(1000,50)% 设置横纵坐标的范围并标上字符
x = 1:0.01:3;
y = x .^ 2;
plot(x,y)  % 画出x和y的图形
axis([0 3 0 10])  % 设置横坐标范围为[0, 3] 纵坐标范围为[0, 10]
pause(3)  % 暂停3秒后再继续接下来的命令
text(2,4,'清风')  % 在坐标为(2,4)的点上标上字符串：清风
close % 关闭图形窗口%% (2) 代码求解
% 1. 不画追击的示意图
clear;clc
v=200; % 任意给定B船的速度（后期我们可以再改的）
dt=0.0000001; % 定义时间间隔
x=[0,20]; % 定义导弹和B船的横坐标分别为x(1)和x(2)
y=[0,0]; % 定义导弹和B船的纵坐标分别为y(1)和y(2)
t=0; % 初始化导弹击落B船的时间
d=0; % 初始化导弹飞行的距离
m=sqrt(2)/2;   % 将sqrt(2)/2定义为一个常量，使后面看起来很简洁
dd=sqrt((x(2)-x(1))^2+(y(2)-y(1))^2); % 导弹与B船的距离
while(dd>=0.001)  % 只要两者的距离足够大，就一直循环下去。（两者距离足够小时表示导弹击中，这里的临界值要结合dt来取，否则可能导致错过交界处的情况）t=t+dt; % 更新导弹击落B船的时间d=d+3*v*dt; % 更新导弹飞行的距离x(2)=20+t*v*m;  y(2)=t*v*m;   % 计算新的B船的位置 （注：m=sqrt(2)/2）dd=sqrt((x(2)-x(1))^2+(y(2)-y(1))^2);  % 更新导弹与B船的距离tan_alpha=(y(2)-y(1))/(x(2)-x(1));   % 计算斜率，即tan(α)cos_alpha=sqrt(1/(1+tan_alpha^2));   % sec(α)^2 = (1+tan(α)^2)sin_alpha=sqrt(1-cos_alpha^2);  % sin(α)^2 +cos(α)^2 = 1x(1)=x(1)+3*v*dt*cos_alpha;   y(1)=y(1)+3*v*dt*sin_alpha; % 计算新的导弹的位置if d>50  % 导弹的有效射程为50个单位disp('导弹没有击中B船');break;  % 退出循环endif d<=50 & dd<0.001   % 导弹飞行的距离小于50个单位且导弹和B船的距离小于0.001（表示击中）disp(['导弹飞行',num2str(d),'单位后击中B船'])disp(['导弹飞行的时间为',num2str(t*60),'分钟'])end
end% 2. 画追击的示意图
clear;clc
v=200; % 任意给定B船的速度（后期我们可以再改的）
dt=0.0000001; % 定义时间间隔
x=[0,20]; % 定义导弹和B船的横坐标分别为x(1)和x(2)
y=[0,0]; % 定义导弹和B船的纵坐标分别为y(1)和y(2)
t=0; % 初始化导弹击落B船的时间
d=0; % 初始化导弹飞行的距离
m=sqrt(2)/2;   % 将sqrt(2)/2定义为一个常量，使后面看起来很简洁
dd=sqrt((x(2)-x(1))^2+(y(2)-y(1))^2); % 导弹与B船的距离
for i=1:2plot(x(i),y(i),'.k','MarkerSize',1);  % 画出导弹和B船所在的坐标，点的大小为1，颜色为黑色(k)，用小点表示grid on;  % 打开网格线hold on;  % 不关闭图形，继续画图
end
axis([0 30 0 10])  % 固定x轴的范围为0-30  固定y轴的范围为0-10
k = 0;  % 引入一个变量  为了控制画图的速度（因为Matlab中画图的速度超级慢）
while(dd>=0.001)  % 只要两者的距离足够大，就一直循环下去。（两者距离足够小时表示导弹击中，这里的临界值要结合dt来取，否则可能导致错过交界处的情况）t=t+dt; % 更新导弹击落B船的时间d=d+3*v*dt; % 更新导弹飞行的距离x(2)=20+t*v*m;  y(2)=t*v*m;   % 计算新的B船的位置 （注：m=sqrt(2)/2）dd=sqrt((x(2)-x(1))^2+(y(2)-y(1))^2);  % 更新导弹与B船的距离tan_alpha=(y(2)-y(1))/(x(2)-x(1));   % 计算斜率，即tan(α)cos_alpha=sqrt(1/(1+tan_alpha^2));   % 利用公式：sec(α)^2 = (1+tan(α)^2)  计算出cos(α)sin_alpha=sqrt(1-cos_alpha^2);  % 利用公式： sin(α)^2 +cos(α)^2 = 1  计算出sin(α)x(1)=x(1)+3*v*dt*cos_alpha;   y(1)=y(1)+3*v*dt*sin_alpha;   % 计算新的导弹的位置k = k +1 ;  if mod(k,500) == 0   % 每刷新500次时间就画出下一个导弹和B船所在的坐标  mod(m,n)表示求m/n的余数for i=1:2plot(x(i),y(i),'.k','MarkerSize',1);hold on; % 不关闭图形，继续画图endpause(0.001);  % 暂停0.001s后再继续下面的操作endif d>50  % 导弹的有效射程为50个单位disp('导弹没有击中B船');break;  % 退出循环endif d<=50 & dd<0.001   % 导弹飞行的距离小于50个单位且导弹和B船的距离小于0.001（表示击中）disp(['导弹飞行',num2str(d),'个单位后击中B船'])disp(['导弹飞行的时间为',num2str(t*60),'分钟'])end
end

效果如下图所示：

6、旅行商问题

一个售货员必须访问n个城市，这n个城市是一个完全图，售货员需要恰好访问所有城市的一次，并且回到最终的城市。城市于城市之间有一个旅行费用，售货员希望旅行费用之和最少。

%% TSP(旅行商问题)
%% （1）预备知识
plot([1,2],[5,10],'-o') % 画出一条线段，x范围是[1, 2] ，y范围是[5,10]
text(1.5,7.5,'清风') % 在坐标(1.5,7.5)处标上文本：清风
close% randperm函数的用法
randperm(5)  % 生成1-5组成的一个随机序列(类似于洗牌的操作)
%      3     5     1     2     4
%      1     4     5     3     2%% （2）代码求解
clear;clc
% 只有10个城市的简单情况coord =[0.6683 0.6195 0.4    0.2439 0.1707 0.2293 0.5171 0.8732 0.6878 0.8488 ;0.2536 0.2634 0.4439 0.1463 0.2293 0.761  0.9414 0.6536 0.5219 0.3609]' ;  % 城市坐标矩阵，n行2列
% 38个城市，TSP数据集网站(http://www.tsp.gatech.edu/world/djtour.html) 上公测的最优结果6656。% coord = [11003.611100,42102.500000;11108.611100,42373.888900;11133.333300,42885.833300;11155.833300,42712.500000;11183.333300,42933.333300;11297.500000,42853.333300;11310.277800,42929.444400;11416.666700,42983.333300;11423.888900,43000.277800;11438.333300,42057.222200;11461.111100,43252.777800;11485.555600,43187.222200;11503.055600,42855.277800;11511.388900,42106.388900;11522.222200,42841.944400;11569.444400,43136.666700;11583.333300,43150.000000;11595.000000,43148.055600;11600.000000,43150.000000;11690.555600,42686.666700;11715.833300,41836.111100;11751.111100,42814.444400;11770.277800,42651.944400;11785.277800,42884.444400;11822.777800,42673.611100;11846.944400,42660.555600;11963.055600,43290.555600;11973.055600,43026.111100;12058.333300,42195.555600;12149.444400,42477.500000;12286.944400,43355.555600;12300.000000,42433.333300;12355.833300,43156.388900;12363.333300,43189.166700;12372.777800,42711.388900;12386.666700,43334.722200;12421.666700,42895.555600;12645.000000,42973.333300];n = size(coord,1);  % 城市的数目figure(1)  % 新建一个编号为1的图形窗口
plot(coord(:,1),coord(:,2),'o');   % 画出城市的分布散点图
for i = 1:ntext(coord(i,1)+0.01,coord(i,2)+0.01,num2str(i))   % 在图上标上城市的编号（加上0.01表示把文字的标记往右上方偏移一点）
end
hold on % 等一下要接着在这个图形上画图的d = zeros(n);   % 初始化两个城市的距离矩阵全为0
for i = 2:n  for j = 1:i  coord_i = coord(i,:);   x_i = coord_i(1);     y_i = coord_i(2);  % 城市i的横坐标为x_i，纵坐标为y_icoord_j = coord(j,:);   x_j = coord_j(1);     y_j = coord_j(2);  % 城市j的横坐标为x_j，纵坐标为y_jd(i,j) = sqrt((x_i-x_j)^2 + (y_i-y_j)^2);   % 计算城市i和j的距离end
end
d = d+d';   % 生成距离矩阵的对称的一面min_result = +inf;  % 假设最短的距离为min_result，初始化为无穷大，后面只要找到比它小的就对其更新
min_path = [1:n];   % 初始化最短的路径就是1-2-3-...-n
N = 10000000;  % 蒙特卡罗模拟的次数
for k = 1:N  % 开始循环result = 0;  % 初始化走过的路程为0path = randperm(n);  % 生成一个1-n的随机打乱的序列for i = 1:n-1  result = d(path(i),path(i+1)) + result;  % 按照这个序列不断的更新走过的路程这个值endresult = d(path(1),path(n)) + result;  % 别忘了加上从最后一个城市返回到最开始那个城市的距离if result < min_result  % 判断这次模拟走过的距离是否小于最短的距离，如果小于就更新最短距离和最短的路径min_path = path;min_result = resultend
end
min_path
min_path = [min_path,min_path(1)];   % 在最短路径的最后面加上一个元素，即第一个点（我们要生成一个封闭的图形）
n = n+1;  % 城市的个数加一个（紧随着上一步）
for i = 1:n-1 j = i+1;coord_i = coord(min_path(i),:);   x_i = coord_i(1);     y_i = coord_i(2); coord_j = coord(min_path(j),:);   x_j = coord_j(1);     y_j = coord_j(2);plot([x_i,x_j],[y_i,y_j],'-')    % 每两个点就作出一条线段，直到所有的城市都走完pause(0.5)  % 暂停0.5s再画下一条线段hold on
end

参考文献： 清风[清风数学建模教程]，仅作为个人笔记。

[数模笔记]蒙特卡罗模拟相关推荐

1. Python数模笔记-StatsModels 统计回归（2）线性回归

   1.背景知识 1.1 插值.拟合.回归和预测 插值.拟合.回归和预测,都是数学建模中经常提到的概念,而且经常会被混为一谈. 插值,是在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数 ...

2. Python数模笔记-模拟退火算法（4）旅行商问题

   1.旅行商问题(Travelling salesman problem, TSP) 旅行商问题是经典的组合优化问题,要求找到遍历所有城市且每个城市只访问一次的最短旅行路线,即对给定的正权完全图求其总权 ...

3. Python数模笔记-模拟退火算法（3）整数规划问题

   1.整数规划问题 整数规划问题在工业.经济.国防.医疗等各行各业应用十分广泛,是指规划中的变量(全部或部分)限制为整数,属于离散优化问题(Discrete Optimization). 线性规划问题的 ...

4. Python数模笔记-模拟退火算法（2）约束条件的处理

   1.最优化与线性规划 最优化问题的三要素是决策变量.目标函数和约束条件. 线性规划(Linear programming),是研究线性约束条件下线性目标函数的极值问题的优化方法,常用于解决利用现有的资 ...

5. Python数模笔记-模拟退火算法（1）多变量函数优化

   1.模拟退火算法 模拟退火算法借鉴了统计物理学的思想,是一种简单.通用的启发式优化算法,并在理论上具有概率性全局优化性能,因而在科研和工程中得到了广泛的应用. 退火是金属从熔融状态缓慢冷却.最终达到能 ...

6. Python数模笔记-NetworkX（4）最小生成树

   1.生成树和最小生成树 1.1 生成树 连通的无圈图称为树,就是不包含循环的回路的连通图. 对于无向连通图,生成树(Spanning tree)是原图的极小连通子图,它包含原图中的所有 n 个顶点,并 ...

7. Python数模笔记-NetworkX（3）条件最短路径

   1.带有条件约束的最短路径问题 最短路径问题是图论中求两个顶点之间的最短路径问题,通常是求最短加权路径. 条件最短路径,指带有约束条件.限制条件的最短路径.例如,顶点约束,包括必经点或禁止点的限制:边 ...

8. Python数模笔记-NetworkX（2）最短路径

   1.最短路径问题的常用算法 最短路径问题是图论研究中的经典算法问题,用于计算图中一个顶点到另一个顶点的最短路径. 欢迎关注 Youcans 原创系列,每周更新数模笔记 Python数模笔记-PuLP库 ...

9. Python数模笔记-NetworkX（1）图的操作

   1.NetworkX 图论与网络工具包 NetworkX 是基于 Python 语言的图论与复杂网络工具包,用于创建.操作和研究复杂网络的结构.动力学和功能. NetworkX 可以以标准和非标准的数 ...

10. Python数模笔记-Sklearn（4）线性回归

    1.什么是线性回归? 回归分析(Regression analysis)是一种统计分析方法,研究自变量和因变量之间的定量关系.回归分析不仅包括建立数学模型并估计模型参数,检验数学模型的可信度,也包括利 ...

最新文章

1. 中国顶级 AI 研究者数量仅为美国 1/5：美国智库最新全球 AI 实力报告
2. 【深度学习】谷歌大脑EfficientNet的工作原理解析
3. crackme之018
4. 【FTP】FTP服务器的搭建
5. python 在python的class中的,self到底是什么？
6. golang之iota
7. 九十五、轻松搞定Python中的Excel办公自动化系列
8. 【Docker-Ubuntu】ubuntu16.04 docker 使用记录
9. hadoop基本思想与概念
10. 如何使用Aimersoft Video Suite Mac将 DVD 刻录到 ISO/DVD 文件夹
11. HDU 4508 湫湫系列故事——减肥记I （2013腾讯编程马拉松初赛第一场）
12. android intent json,如何从android中的Intent服务中的服务器获取Json响应？
13. MacOS串口调试工具minicom配置
14. 数学作图工具_分别用于教学、排版、科研的数学作图软件
15. 【tensorrt】——error: #error The version of CUB in your include path is not compatible with this releas
16. 【zznu-夏季队内积分赛3-G】2333
17. jvm的类加载和运行时数据区和垃圾回收
18. python 爬虫登录
19. 投资30亿美元 IBM启动云计算大数据芯片研究计划
20. android studio 立即拨打电话程序设计

热门文章

1. CVE-2017-11882：Microsoft office 公式编辑器 font name 字段栈溢出通杀漏洞调试分析
2. 网站换服务器会降权,网站更换IP地址，对SEO有什么影响？
3. python画航线图_数据可视化：python调用pyecharts库绘制航线专题图
4. 在delphi中调用chm帮助文件_delphi教程
5. 华硕afudos刷bios_ASUS主板刷BIOS详细图解方法 包含windows和DOS两种环境
6. web打印的最佳方案
7. 关于Hibernate ResultTransformer
8. matlab参数方程求导 求不定积分
9. 游戏检测到计算机性能过低,windows检测到您的计算机性能缓慢
10. java商城答辩_java网上商城系统毕业设计答辩.ppt