深度学习入门---PCA，白化

引言

主成分分析（PCA）是一种能够极大提升无监督特征学习速度的数据降维算法。更重要的是，理解PCA算法，对实现白化算法有很大的帮助，很多算法都先用白化算法作预处理步骤。
假设你使用图像来训练算法，因为图像中相邻的像素高度相关，输入数据是有一定冗余的。具体来说，假如我们正在训练的16x16灰度值图像，记为一个256维向量 x∈R256 \textstyle x \in \Re^{256} ，其中特征值 xj \textstyle x_j 对应每个像素的亮度值。由于相邻像素间的相关性，PCA算法可以将输入向量转换为一个维数低很多的近似向量，而且误差非常小。

假设我们拥有数据 {x(1),x(2),…,x(m)} \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} ，维度 n=2 \textstyle n=2，即 x(i)∈R2 \textstyle x^{(i)} \in \Re^2 。假设我们想把数据从2维降到1维。（在实际应用中，我们也许需要把数据从256维降到50维；在这里使用低维数据，主要是为了更好地可视化算法的行为）。下图是我们的数据集：

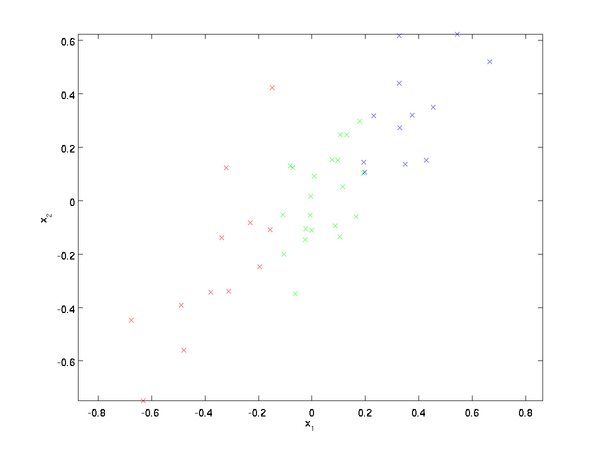
这些数据已经进行了预处理，使得每个特征 x1 \textstyle x_1 和 x2 \textstyle x_2 具有相同的均值（零）和方差。
为方便展示，根据 x1 \textstyle x_1 值的大小，我们将每个点分别涂上了三种颜色之一，但该颜色并不用于算法而仅用于图解。
PCA算法将寻找一个低维空间来投影我们的数据。从下图中可以看出， u1 \textstyle u_1 是数据变化的主方向，而 u2 \textstyle u_2 是次方向

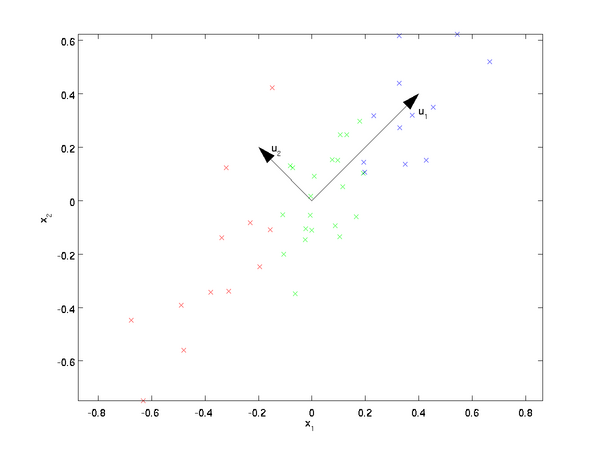
也就是说，数据在 u1 \textstyle u_1 方向上的变化要比在 u2 \textstyle u_2 方向上大。为更形式化地找出方向 u1 \textstyle u_1 和 u2 \textstyle u_2 ，我们首先计算出矩阵 Σ \textstyle \Sigma ，如下所示：

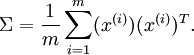
实际上在代码实现时，上面的 x(i) x^{(i)}对应是全部数据集，样本按列摆放。

假设 x \textstyle x 的均值为零，那么 Σ \textstyle \Sigma 就是x的协方差矩阵。（符号 Σ \textstyle \Sigma ，读”Sigma”，是协方差矩阵的标准符号。虽然看起来与求和符号 ∑ni=1i \sum_{i=1}^n i 比较像，但它们其实是两个不同的概念。）

可以证明，数据变化的主方向 u1 \textstyle u_1 就是协方差矩阵 Σ \textstyle \Sigma 的主特征向量，而 u2 \textstyle u_2 是次特征向量。

求得协方差矩阵后，我们需要求出其对应的特征向量组成的矩阵U，按列摆放。

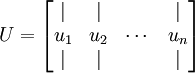
此处， u1 \textstyle u_1 是主特征向量（对应最大的特征值）， u2 \textstyle u_2 是次特征向量。以此类推，另记 λ1,λ2,…,λn \textstyle \lambda_1, \lambda_2, \ldots, \lambda_n 为相应的特征值。
在本例中，向量 u1和u2 \textstyle u_1 和 \textstyle u_2 构成了一个新基，可以用来表示数据。令 x∈R2 \textstyle x \in \Re^2 为训练样本，那么 uT1x \textstyle u_1^Tx 就是样本点 x \textstyle x 在维度 u1 \textstyle u_1 上的投影的长度（幅值）。同样的， uT2x \textstyle u_2^Tx 是 x \textstyle x 投影到 u2 \textstyle u_2 维度上的幅值。

旋转数据

至此，我们可以把 x \textstyle x 用 (u1,u2) \textstyle (u_1, u_2) 基表达为：

xrot=UTx=[uT1xuT2x]

\begin{align} x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^Tx \\ u_2^Tx \end{bmatrix} \end{align}
（下标“rot”来源于单词“rotation”，意指这是原数据经过旋转（也可以说成映射）后得到的结果）

对数据集中的每个样本 i \textstyle i 分别进行旋转： x(i)rot=UTx(i) \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)} for every i \textstyle i ，然后把变换后的数据 xrot \textstyle x_{\rm rot} 显示在坐标图上，可得：

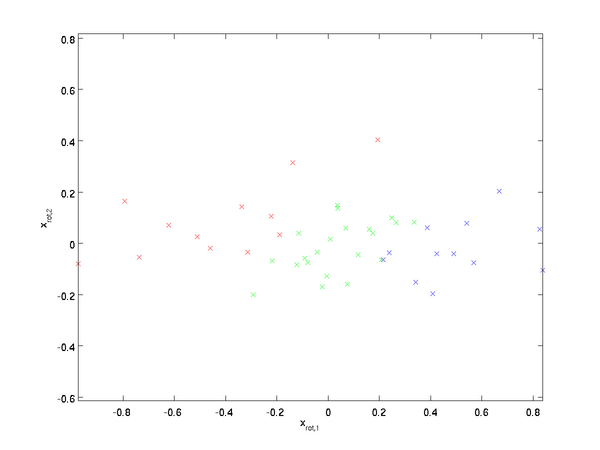
这就是把训练数据集旋转到 u1，u2 \textstyle u_1，\textstyle u_2 基后的结果。一般而言，运算 UTx \textstyle U^Tx 表示旋转到基 u1,u2,...,un \textstyle u_1,\textstyle u_2, ...,\textstyle u_n 之上的训练数据。矩阵 U \textstyle U 有正交性，即满足 UTU=UUT=I \textstyle U^TU = UU^T = I ，所以若想将旋转后的向量 xrot \textstyle x_{\rm rot} 还原为原始数据 x \textstyle x ，将其左乘矩阵 U \textstyle U即可： x=Uxrot \textstyle x=U x_{\rm rot} , 验算一下： Uxrot=UUTx=x. \textstyle U x_{\rm rot} = UU^T x = x.

数据降维

数据的主方向就是旋转数据的第一维 xrot,1 \textstyle x_{{\rm rot},1} 。因此，若想把这数据降到一维，可令：

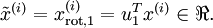
更一般的，假如想把数据 x∈Rn降到k \textstyle x \in \Re^n 降到 \textstyle k 维表示 x~∈Rk（令k<n） \textstyle \tilde{x} \in \Re^k （令 \textstyle k ,只需选取 xrot \textstyle x_{\rm rot} 的前 k \textstyle k 个成分，分别对应前 k \textstyle k 个数据变化的主方向。

PCA的另外一种解释是： xrot \textstyle x_{\rm rot} 是一个 n \textstyle n 维向量，其中前几个成分可能比较大（例如，上例中大部分样本第一个成分 x(i)rot,1=uT1x(i) \textstyle x_{{\rm rot},1}^{(i)} = u_1^Tx^{(i)} 的取值相对较大），而后面成分可能会比较小（例如，上例中大部分样本的 x(i)rot,2=uT2x(i) \textstyle x_{{\rm rot},2}^{(i)} = u_2^Tx^{(i)} 较小）。

PCA算法做的其实就是丢弃 xrot \textstyle x_{\rm rot} 中后面（取值较小）的成分，就是将这些成分的值近似为零。具体的说，设 x~是xrot \textstyle \tilde{x} 是 \textstyle x_{{\rm rot}} 的近似表示，那么将 xrot \textstyle x_{{\rm rot}} 除了前 k \textstyle k 个成分外，其余全赋值为零，就得到：

x~=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢xrot,1⋮xrot,k0⋮0⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥≈⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢xrot,1⋮xrot,kxrot,k+1⋮xrot,n⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥=xrot

\begin{align} \tilde{x} = \begin{bmatrix} x_{{\rm rot},1} \\ \vdots \\ x_{{\rm rot},k} \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} \approx \begin{bmatrix} x_{{\rm rot},1} \\ \vdots \\ x_{{\rm rot},k} \\ x_{{\rm rot},k+1} \\ \vdots \\ x_{{\rm rot},n} \end{bmatrix} = x_{\rm rot} \end{align}
在本例中，可得 x~ \textstyle \tilde{x} 的点图如下（取 n=2,k=1 \textstyle n=2, k=1 ）：

然而，由于上面 x~的后n−k \textstyle \tilde{x} 的后\textstyle n-k项均为零，没必要把这些零项保留下来。所以，我们仅用前 k \textstyle k 个（非零）成分来定义 k \textstyle k 维向量 x~ \textstyle \tilde{x} 。

这也解释了我们为什么会以 u1,u2,…,un \textstyle u_1, u_2, \ldots, u_n 为基来表示数据：要决定保留哪些成分变得很简单，只需取前 k \textstyle k 个成分即可。这时也可以说，我们“保留了前 k \textstyle k 个PCA（主）成分”。

还原近似数据

现在，我们得到了原始数据 x∈Rn \textstyle x \in \Re^n 的低维“压缩”表征量 x~∈Rk \textstyle \tilde{x} \in \Re^k ，反过来，如果给定 x~ \textstyle \tilde{x} ，我们应如何还原原始数据 x \textstyle x 呢？查看以往章节以往章节可知，要转换回来，只需 x=Uxrot \textstyle x = U x_{\rm rot} 即可。进一步，我们把 x~ \textstyle \tilde{x} 看作将 xrot \textstyle x_{\rm rot} 的最后 n−k \textstyle n-k 个元素被置0所得的近似表示，因此如果给定 x~∈Rk \textstyle \tilde{x} \in \Re^k ，可以通过在其末尾添加 n−k个0 \textstyle n-k 个0来得到对 xrot∈Rn \textstyle x_{\rm rot} \in \Re^n 的近似，最后，左乘 U \textstyle U 便可近似还原出原数据 x \textstyle x 。具体来说，计算如下：

x^=U⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢x~1⋮x~k0⋮0⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥=∑i=1kuix~i.

\begin{align} \hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^k u_i \tilde{x}_i. \end{align}
上面的等式基于先前对 \textstyle U 的定义。在实现时，我们实际上并不先给 x~ \textstyle \tilde{x} 填0然后再左乘 U \textstyle U ，因为这意味着大量的乘0运算。我们可用 x~∈Rk \textstyle \tilde{x} \in \Re^k 来与 U \textstyle U 的前 k \textstyle k 列相乘，即上式中最右项，来达到同样的目的。将该算法应用于本例中的数据集，可得如下关于重构数据 x^ \textstyle \hat{x} 的点图：

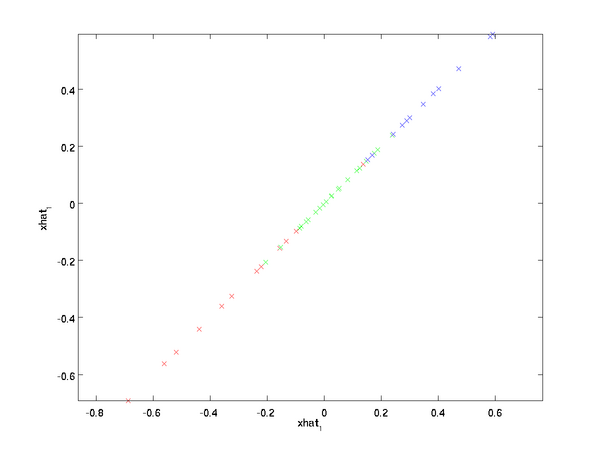
由图可见，我们得到的是对原始数据集的一维近似重构。
在训练自动编码器或其它无监督特征学习算法时，算法运行时间将依赖于输入数据的维数。若用 x~∈Rk \textstyle \tilde{x} \in \Re^k 取代 x \textstyle x 作为输入数据，那么算法就可使用低维数据进行训练，运行速度将显著加快。对于很多数据集来说，低维表征量 x~ \textstyle \tilde{x} 是原数据集的极佳近似，因此在这些场合使用PCA是很合适的，它引入的近似误差的很小，却可显著地提高你算法的运行速度。

选择主成分个数

我们该如何选择 k \textstyle k ，即保留多少个PCA主成分？在上面这个简单的二维实验中，保留第一个成分看起来是自然的选择。对于高维数据来说，做这个决定就没那么简单：如果 k \textstyle k 过大，数据压缩率不高，在极限情况 k=n \textstyle k=n 时，等于是在使用原始数据（只是旋转投射到了不同的基）；相反地，如果 k \textstyle k 过小，那数据的近似误差太太。
决定 k \textstyle k 值时，我们通常会考虑不同 k \textstyle k 值可保留的方差百分比。具体来说，如果 k=n \textstyle k=n ，那么我们得到的是对数据的完美近似，也就是保留了100%的方差，即原始数据的所有变化都被保留下来；相反，如果 k=0 \textstyle k=0 ，那等于是使用零向量来逼近输入数据，也就是只有0%的方差被保留下来。
一般而言，设 λ1,λ2,…,λn \textstyle \lambda_1, \lambda_2, \ldots, \lambda_n 表示 Σ \textstyle \Sigma 的特征值（按由大到小顺序排列），使得 λj \textstyle \lambda_j 为对应于特征向量 uj \textstyle u_j 的特征值。那么如果我们保留前 k \textstyle k 个成分，则保留的方差百分比可计算为：

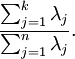
在上面简单的二维实验中， λ1=7.29，λ2=0.69。 \textstyle \lambda_1 = 7.29 ，\textstyle \lambda_2 = 0.69 。因此，如果保留 k=1 \textstyle k=1 个主成分，等于我们保留了 7.29/(7.29+0.69)=0.913 \textstyle 7.29/(7.29+0.69) = 0.913 ，即91.3%的方差。
对保留方差的百分比进行更正式的定义已超出了本教程的范围，但很容易证明， λj=∑mi=1x2rot,j \textstyle \lambda_j = \sum_{i=1}^m x_{{\rm rot},j}^2 。因此，如果 λj≈0，则说明xrot,j \textstyle \lambda_j \approx 0 ，则说明 \textstyle x_{{\rm rot},j} 也就基本上接近于0，所以用0来近似它并不会产生多大损失。这也解释了为什么要保留前面的主成分（对应的 λj \textstyle \lambda_j 值较大）而不是末尾的那些。这些前面的主成分 xrot,j \textstyle x_{{\rm rot},j} 变化性更大，取值也更大，如果将其设为0势必引入较大的近似误差。
以处理图像数据为例，一个惯常的经验法则是选择 \textstyle k 以保留99%的方差，换句话说，我们选取满足以下条件的最小 k \textstyle k 值：

∑kj=1λj∑nj=1λj≥0.99.

\begin{align} \frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j} \geq 0.99. \end{align}
对其它应用，如不介意引入稍大的误差，有时也保留90-98%的方差范围。若向他人介绍PCA算法详情，告诉他们你选择的 k \textstyle k 保留了95%的方差，比告诉他们你保留了前120个（或任意某个数字）主成分更好理解。

对图像数据应用PCA算法

为使PCA算法能有效工作，通常我们希望所有的特征 x1,x2,…,xn \textstyle x_1, x_2, \ldots, x_n 都有相似的取值范围（并且均值接近于0）。如果你曾在其它应用中使用过PCA算法，你可能知道有必要单独对每个特征做预处理，即通过估算每个特征 xj \textstyle x_j 的均值和方差，而后将其取值范围规整化为零均值和单位方差。但是，对于大部分图像类型，我们却不需要进行这样的预处理。假定我们将在自然图像上训练算法，此时特征 xj \textstyle x_j 代表的是像素 j \textstyle j 的值。所谓“自然图像”，不严格的说，是指人或动物在他们一生中所见的那种图像。
注：通常我们选取含草木等内容的户外场景图片，然后从中随机截取小图像块（如16x16像素）来训练算法。在实践中我们发现，大多数特征学习算法对训练图片的确切类型并不敏感，所以大多数用普通照相机拍摄的图片，只要不是特别的模糊或带有非常奇怪的人工痕迹，都可以使用。
在自然图像上进行训练时，对每一个像素单独估计均值和方差意义不大，因为（理论上）图像任一部分的统计性质都应该和其它部分相同，图像的这种特性被称作平稳性（stationarity）。
具体而言，为使PCA算法正常工作，我们通常需要满足以下要求：(1)特征的均值大致为0；(2)不同特征的方差值彼此相似。对于自然图片，即使不进行方差归一化操作，条件(2)也自然满足，故而我们不再进行任何方差归一化操作（对音频数据,如声谱,或文本数据,如词袋向量，我们通常也不进行方差归一化）。实际上，PCA算法对输入数据具有缩放不变性，无论输入数据的值被如何放大（或缩小），返回的特征向量都不改变。更正式的说：如果将每个特征向量 x \textstyle x 都乘以某个正数（即所有特征量被放大或缩小相同的倍数），PCA的输出特征向量都将不会发生变化。
既然我们不做方差归一化，唯一还需进行的规整化操作就是均值规整化，其目的是保证所有特征的均值都在0附近。根据应用，在大多数情况下，我们并不关注所输入图像的整体明亮程度。比如在对象识别任务中，图像的整体明亮程度并不会影响图像中存在的是什么物体。更为正式地说，我们对图像块的平均亮度值不感兴趣，所以可以减去这个值来进行均值规整化。
具体的步骤是，如果 x(i)∈Rn \textstyle x^{(i)} \in \Re^{n} 代表16x16的图像块的亮度（灰度）值（ n=256 \textstyle n=256 ），可用如下算法来对每幅图像进行零均值化操作：
μ(i):=1n∑nj=1x(i)j \mu^{(i)} := \frac{1}{n} \sum_{j=1}^n x^{(i)}_j
x(i)j:=x(i)j−μ(i),forallj x^{(i)}_j := x^{(i)}_j - \mu^{(i)}, for all \textstyle j

请注意：1）对每个输入图像块 x(i) \textstyle x^{(i)} 都要单独执行上面两个步骤，2）这里的 μ(i) \textstyle \mu^{(i)} 是指图像块 x(i) \textstyle x^{(i)} 的平均亮度值。尤其需要注意的是，这和为每个像素 xj \textstyle x_j 单独估算均值是两个完全不同的概念。
如果你处理的图像并非自然图像（比如，手写文字，或者白背景正中摆放单独物体），其他规整化操作就值得考虑了，而哪种做法最合适也取决于具体应用场合。但对自然图像而言，对每幅图像进行上述的零均值规整化，是默认而合理的处理。

PCA白化

我们已经了解了如何使用PCA降低数据维度。在一些算法中还需要一个与之相关的预处理步骤，这个预处理过程称为白化（一些文献中也叫sphering）。举例来说，假设训练数据是图像，由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性；更正式的说，我们希望通过白化过程使得学习算法的输入具有如下性质：(i)特征之间相关性较低；(ii)所有特征具有相同的方差。

如何消除输入特征之间的相关性? 在前文计算 x(i)rot=UTx(i) \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)} 时实际上已经消除了输入特征 x(i) \textstyle x^{(i)}之间的相关性。得到的新特征 xrot \textstyle x_{\rm rot} 的分布如下图所示：

这个数据的协方差矩阵如下：

[7.29000.69].

\begin{align} \begin{bmatrix} 7.29 & 0 \\ 0 & 0.69 \end{bmatrix}. \end{align}
(注: 严格地讲, 这部分许多关于“协方差”的陈述仅当数据均值为0时成立。下文的论述都隐式地假定这一条件成立。不过即使数据均值不为0，下文的说法仍然成立，所以你无需担心这个。)

xrot \textstyle x_{\rm rot} 协方差矩阵对角元素的值为 λ1 \textstyle \lambda_1 和 λ2 \textstyle \lambda_2 绝非偶然。并且非对角元素值为0; 因此, xrot,1和xrot,2 \textstyle x_{{\rm rot},1} 和 \textstyle x_{{\rm rot},2} 是不相关的, 满足我们对白化结果的第一个要求 (特征间相关性降低)。
为了使每个输入特征具有单位方差，我们可以直接使用 1/λi−−√ \textstyle 1/\sqrt{\lambda_i} 作为缩放因子来缩放每个特征 xrot,i \textstyle x_{{\rm rot},i} 。具体地，我们定义白化后的数据 xPCAwhite∈Rn \textstyle x_{{\rm PCAwhite}} \in \Re^n 如下：

xPCAwhite,i=xrot,iλi−−√.

\begin{align} x_{{\rm PCAwhite},i} = \frac{x_{{\rm rot},i} }{\sqrt{\lambda_i}}. \end{align}

绘制出 xPCAwhite \textstyle x_{{\rm PCAwhite}} ，我们得到:

这些数据现在的协方差矩阵为单位矩阵 I \textstyle I 。我们说， xPCAwhite \textstyle x_{{\rm PCAwhite}} 是数据经过PCA白化后的版本: xPCAwhite \textstyle x_{{\rm PCAwhite}} 中不同的特征之间不相关并且具有单位方差。
白化与降维相结合。如果你想要得到经过白化后的数据，并且比初始输入维数更低,可以仅保留 xPCAwhite \textstyle x_{{\rm PCAwhite}} 中前 k \textstyle k 个成分。当我们把PCA白化和正则化结合起来时(在稍后讨论)， xPCAwhite \textstyle x_{{\rm PCAwhite}} 中最后的少量成分将总是接近于0，因而舍弃这些成分不会带来很大的问题。

ZCA白化

最后要说明的是，使数据的协方差矩阵变为单位矩阵 I \textstyle I 的方式并不唯一。具体地，如果 R \textstyle R 是任意正交矩阵，即满足 RRT=RTR=I \textstyle RR^T = R^TR = I (说它正交不太严格， R \textstyle R 可以是旋转或反射矩阵), 那么 RxPCAwhite \textstyle R \,x_{\rm PCAwhite} 仍然具有单位协方差。在ZCA白化中，令 R=U \textstyle R = U 。我们定义ZCA白化的结果为：

xZCAwhite=UxPCAwhite

\begin{align} x_{\rm ZCAwhite} = U x_{\rm PCAwhite} \end{align}
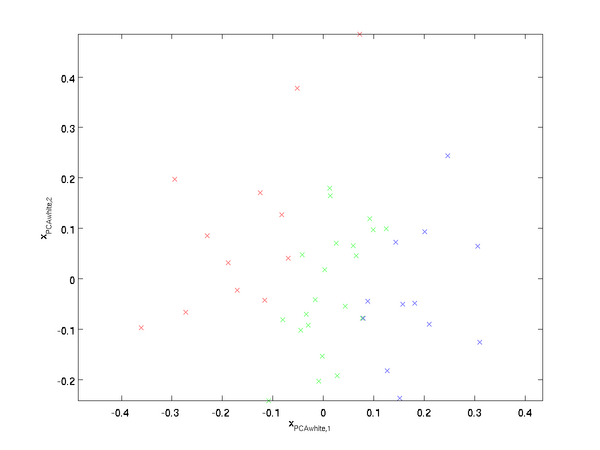
绘制 xZCAwhite \textstyle x_{\rm ZCAwhite}，得到:

可以证明，对所有可能的 R \textstyle R，这种旋转使得 xZCAwhite \textstyle x_{\rm ZCAwhite} 尽可能地接近原始输入数据 x \textstyle x 。
当使用 ZCA白化时(不同于 PCA白化)，我们通常保留数据的全部 n \textstyle n 个维度，不尝试去降低它的维数。

正则化

实践中需要实现PCA白化或ZCA白化时，有时一些特征值 λi \textstyle \lambda_i 在数值上接近于0，这样在缩放步骤时我们除以 λi−−√ \sqrt{\lambda_i} 将导致除以一个接近0的值；这可能使数据上溢 (赋为大数值)或造成数值不稳定。因而在实践中，我们使用少量的正则化实现这个缩放过程，即在取平方根和倒数之前给特征值加上一个很小的常数 \textstyle \epsilon：

xPCAwhite,i=xrot,iλi+ϵ−−−−−√.

\begin{align} x_{{\rm PCAwhite},i} = \frac{x_{{\rm rot},i} }{\sqrt{\lambda_i + \epsilon}}. \end{align}
当 x \textstyle x 在区间 [−1,1] \textstyle [-1,1] 上时, 一般取值为 ϵ≈10−5 \textstyle \epsilon \approx 10^{-5}。
对图像来说, 这里加上 ϵ \textstyle \epsilon ，对输入图像也有一些平滑(或低通滤波)的作用。这样处理还能消除在图像的像素信息获取过程中产生的噪声，改善学习到的特征(细节超出了本文的范围)。

ZCA 白化是一种数据预处理方法，它将数据从 x \textstyle x 映射到 xZCAwhite \textstyle x_{\rm ZCAwhite} 。事实证明这也是一种生物眼睛(视网膜)处理图像的粗糙模型。具体而言，当你的眼睛感知图像时，由于一幅图像中相邻的部分在亮度上十分相关，大多数临近的“像素”在眼中被感知为相近的值。因此，如果人眼需要分别传输每个像素值（通过视觉神经）到大脑中，会非常不划算。取而代之的是，视网膜进行一个与ZCA中相似的去相关操作 (这是由视网膜上的ON-型和OFF-型光感受器细胞将光信号转变为神经信号完成的)。由此得到对输入图像的更低冗余的表示，并将它传输到大脑。