python计算定积分_python编程通过蒙特卡洛法计算定积分详解

这篇文章主要介绍了python编程通过蒙特卡洛法计算定积分详解，具有一定借鉴价值，需要的朋友可以参考下。

想当初，考研的时候要是知道有这么个好东西，计算定积分。。。开玩笑，那时候计算定积分根本没有这么简单的。但这确实给我打开了一种思路，用编程语言去解决更多更复杂的数学问题。下面进入正题。

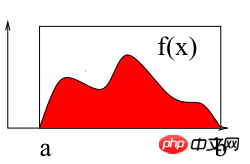
如上图所示，计算区间[a b]上f(x)的积分即求曲线与X轴围成红色区域的面积。下面使用蒙特卡洛法计算区间[2 3]上的定积分：∫(x2+4*x*sin(x))dx

# -*- coding: utf-8 -*-

import numpy as np

import matplotlib.pyplot as plt

def f(x):

return x**2 + 4*x*np.sin(x)

def intf(x):

return x**3/3.0+4.0*np.sin(x) - 4.0*x*np.cos(x)

a = 2;

b = 3;

# use N draws

N= 10000

X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b

Y =f(X) # CALCULATE THE f(x)

# 蒙特卡洛法计算定积分：面积=宽度*平均高度

Imc= (b-a) * np.sum(Y)/ N;

exactval=intf(b)-intf(a)

print "Monte Carlo estimation=",Imc, "Exact number=", intf(b)-intf(a)

# --How does the accuracy depends on the number of points(samples)? Lets try the same 1-D integral

# The Monte Carlo methods yield approximate answers whose accuracy depends on the number of draws.

Imc=np.zeros(1000)

Na = np.linspace(0,1000,1000)

exactval= intf(b)-intf(a)

for N in np.arange(0,1000):

X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b

Y =f(X) # CALCULATE THE f(x)

Imc[N]= (b-a) * np.sum(Y)/ N;

plt.plot(Na[10:],np.sqrt((Imc[10:]-exactval)**2), alpha=0.7)

plt.plot(Na[10:], 1/np.sqrt(Na[10:]), 'r')

plt.xlabel("N")

plt.ylabel("sqrt((Imc-ExactValue)$^2$)")

plt.show()

>>>

Monte Carlo estimation= 11.8181144118 Exact number= 11.8113589251

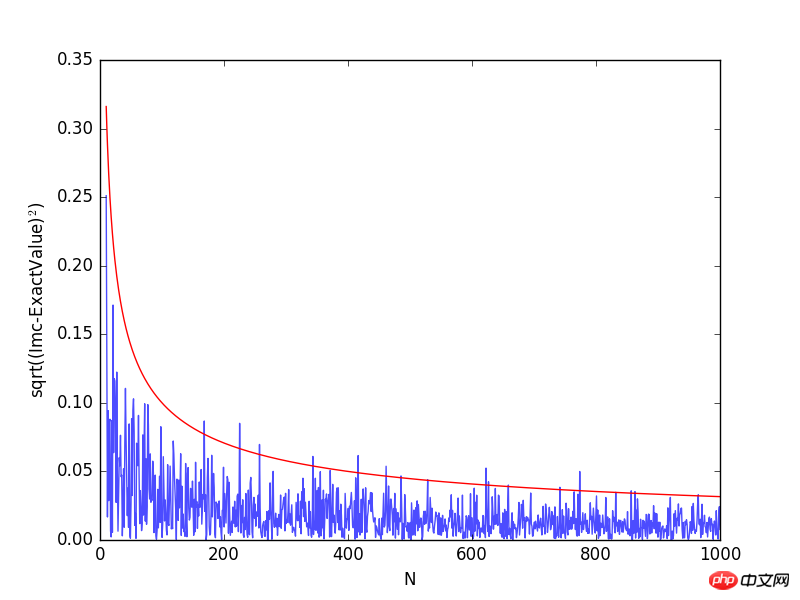
从上图可以看出，随着采样点数的增加，计算误差逐渐减小。想要提高模拟结果的精确度有两个途径：其一是增加试验次数N；其二是降低方差σ2. 增加试验次数势必使解题所用计算机的总时间增加，要想以此来达到提高精度之目的显然是不合适的。下面来介绍重要抽样法来减小方差，提高积分计算的精度。

重要性抽样法的特点在于，它不是从给定的过程的概率分布抽样，而是从修改的概率分布抽样，使对模拟结果有重要作用的事件更多出现，从而提高抽样效率，减少花费在对模拟结果无关紧要的事件上的计算时间。比如在区间[a b]上求g(x)的积分，若采用均匀抽样，在函数值g(x)比较小的区间内产生的抽样点跟函数值较大处区间内产生的抽样点的数目接近，显然抽样效率不高，可以将抽样概率密度函数改为f(x)，使f(x)与g(x)的形状相近，就可以保证对积分计算贡献较大的抽样值出现的机会大于贡献小的抽样值，即可以将积分运算改写为：

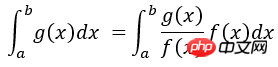
x是按照概率密度f(x)抽样获得的随机变量，显然在区间[a b]内应该有：

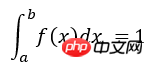
因此，可容易将积分值I看成是随机变量 Y = g(x)/f(x)的期望，式子中xi是服从概率密度f(x)的采样点

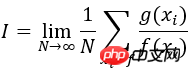
下面的例子采用一个正态分布函数f(x)来近似g(x)=sin(x)*x，并依据正态分布选取采样值计算区间[0 pi]上的积分个∫g(x)dx

# -*- coding: utf-8 -*-

# Example: Calculate ∫sin(x)xdx

# The function has a shape that is similar to Gaussian and therefore

# we choose here a Gaussian as importance sampling distribution.

from scipy import stats

from scipy.stats import norm

import numpy as np

import matplotlib.pyplot as plt

mu = 2;

sig =.7;

f = lambda x: np.sin(x)*x

infun = lambda x: np.sin(x)-x*np.cos(x)

p = lambda x: (1/np.sqrt(2*np.pi*sig**2))*np.exp(-(x-mu)**2/(2.0*sig**2))

normfun = lambda x: norm.cdf(x-mu, scale=sig)

plt.figure(figsize=(18,8)) # set the figure size

# range of integration

xmax =np.pi

xmin =0

# Number of draws

N =1000

# Just want to plot the function

x=np.linspace(xmin, xmax, 1000)

plt.subplot(1,2,1)

plt.plot(x, f(x), 'b', label=u'Original $x\sin(x)$')

plt.plot(x, p(x), 'r', label=u'Importance Sampling Function: Normal')

plt.xlabel('x')

plt.legend()

# =============================================

# EXACT SOLUTION

# =============================================

Iexact = infun(xmax)-infun(xmin)

print Iexact

# ============================================

# VANILLA MONTE CARLO

# ============================================

Ivmc = np.zeros(1000)

for k in np.arange(0,1000):

x = np.random.uniform(low=xmin, high=xmax, size=N)

Ivmc[k] = (xmax-xmin)*np.mean(f(x))

# ============================================

# IMPORTANCE SAMPLING

# ============================================

# CHOOSE Gaussian so it similar to the original functions

# Importance sampling: choose the random points so that

# more points are chosen around the peak, less where the integrand is small.

Iis = np.zeros(1000)

for k in np.arange(0,1000):

# DRAW FROM THE GAUSSIAN: xis~N(mu,sig^2)

xis = mu + sig*np.random.randn(N,1);

xis = xis[ (xisxmin)] ;

# normalization for gaussian from 0..pi

normal = normfun(np.pi)-normfun(0) # 注意:概率密度函数在采样区间[0 pi]上的积分需要等于1

Iis[k] =np.mean(f(xis)/p(xis))*normal # 因此,此处需要乘一个系数即p(x)在[0 pi]上的积分

plt.subplot(1,2,2)

plt.hist(Iis,30, histtype='step', label=u'Importance Sampling');

plt.hist(Ivmc, 30, color='r',histtype='step', label=u'Vanilla MC');

plt.vlines(np.pi, 0, 100, color='g', linestyle='dashed')

plt.legend()

plt.show()

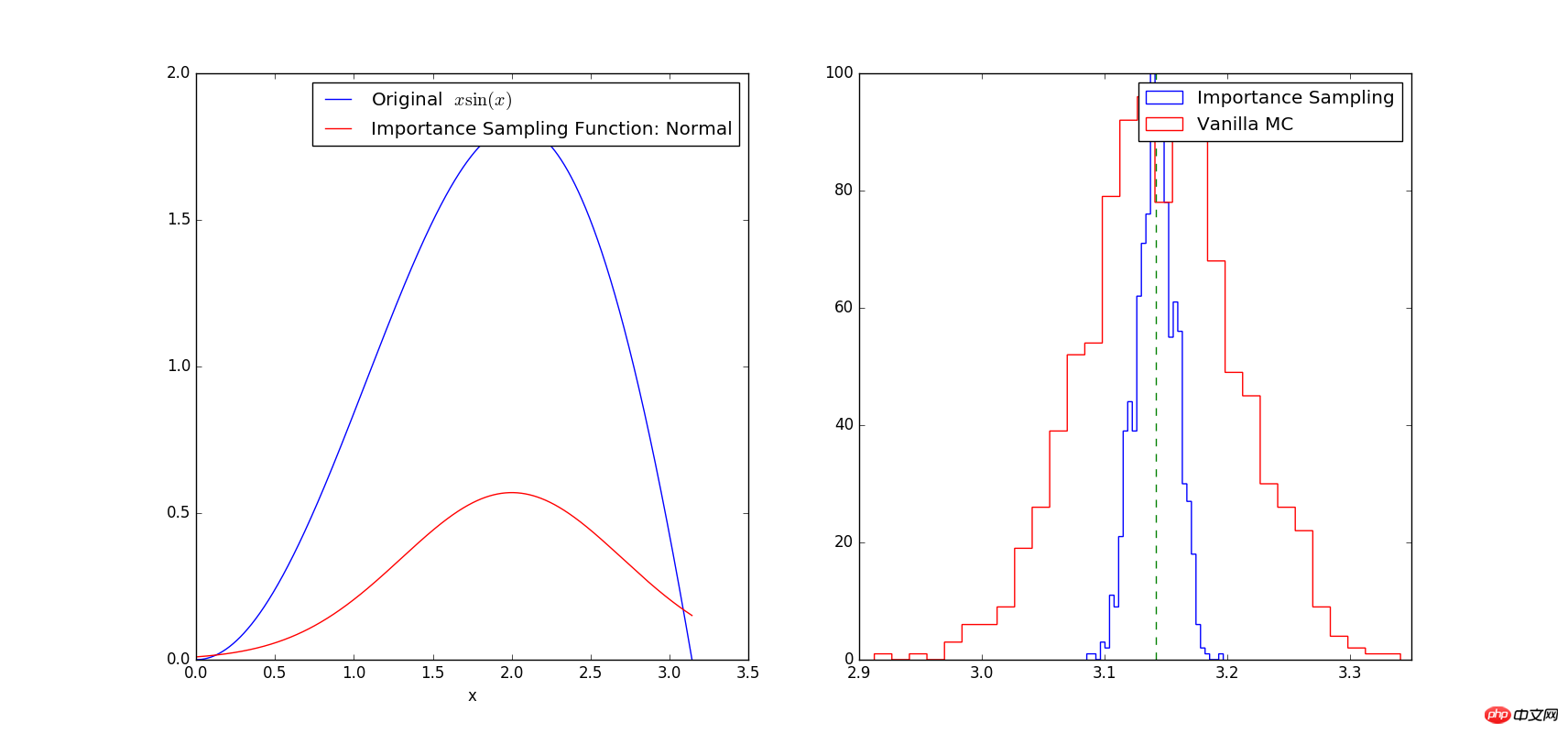
从图中可以看出曲线sin(x)*x的形状和正态分布曲线的形状相近，因此在曲线峰值处的采样点数目会比曲线上位置低的地方要多。精确计算的结果为pi，从上面的右图中可以看出：两种方法均计算定积分1000次，靠近精确值pi=3.1415处的结果最多，离精确值越远数目越少，显然这符合常规。但是采用传统方法(红色直方图)计算出的积分值方的差明显比采用重要抽样法(蓝色直方图)要大。因此，采用重要抽样法计算可以降低方差，提高精度。另外需要注意的是：关于函数f(x)的选择会对计算结果的精度产生影响，当我们选择的函数f(x)与g(x)相差较大时，计算结果的方差也会加大。

python计算定积分_python编程通过蒙特卡洛法计算定积分详解相关推荐

python用蒙特卡洛法区间_python编程通过蒙特卡洛法计算定积分详解
想当初,考研的时候要是知道有这么个好东西,计算定积分...开玩笑,那时候计算定积分根本没有这么简单的.但这确实给我打开了一种思路,用编程语言去解决更多更复杂的数学问题.下面进入正题. 如上图所示,计算 ...
python 自动化发送邮件_Python自动化必备发送邮件报告脚本详解
#!/usr/bin/python3 # -*- coding:UTF-8 -*- import smtplib #smtplib库主要用来连接第三方smtp库,用来发邮件 from email.mi ...
如何在python制作计算器_Python简易计算器制作方法代码详解
主要用到的工具是Python中的Tkinter库比较简单直接上图形界面和代码引用Tkinter库 from tkinter import * 建立主窗口对象 window=Tk() #设置窗口对 ...
python深拷贝一个对象_Python对象的深拷贝和浅拷贝详解
本文内容是在<Python核心编程2>上看到的,感觉很有用便写出来,给大家参考参考! 浅拷贝首先我们使用两种方式来拷贝对象,一种是切片,另外一种是工厂方法.然后使用id函数来看看它们的标 ...
python数据清洗实例_python 数据的清理行为实例详解
python 数据的清理行为实例详解数据清洗主要是指填充缺失数据,消除噪声数据等操作,主要还是通过分析"脏数据"产生的原因和存在形式,利用现有的数据挖掘手段去清洗"脏数 ...
python xlrd课程_python中xlrd模块的使用详解
一.xlrd的安装打开cmd输入pip install xlrd安装完成即可二.xlrd模块的使用下面以这个工作簿为例 1.导入模块 import xlrd 2.打开工作薄 # filename ...
python echarts接口_python绘图pyecharts+pandas的使用详解
pyecharts介绍 pyecharts 是一个用于生成 Echarts 图表的类库.Echarts 是百度开源的一个数据可视化 JS 库.用 Echarts 生成的图可视化效果非常棒为避免绘制缺 ...
python linspace函数_python的range和linspace使用详解
在python中要产生一个数字序列,最快的方法就是使用range和linspace函数,但是这两者不太一样,但总的来说实现的效果是一致的,都能获取一个数字序列. range range一看其名就知道是 ...
python多态的例子_Python编程之多态用法实例详解
本文实例讲述了Python编程之多态用法.分享给大家供大家参考.具体分析如下: 什么是多态?顾名思义,多态就是多种表现形态的意思.它是一种机制.一种能力,而非某个关键字.它在类的继承中得以实现,在类的 ...

python计算定积分_python编程通过蒙特卡洛法计算定积分详解

python计算定积分_python编程通过蒙特卡洛法计算定积分详解相关推荐

最新文章

热门文章