机器学习--＞贝叶斯网络

本篇博文主要总结贝叶斯网络相关知识。

复习之前的知识点

相对熵

相对熵，又称互熵，交叉熵，鉴别信息， K u l l b a c k Kullback Kullback 熵， K u l l b a c k − L e i b l e Kullback-Leible Kullback−Leible 散度等。

设 p ( x ) 、 q ( x ) p(x)、q(x) p(x)、q(x) 是 X X X 中取值的两个概率分布，则 p p p 对 q q q 的相对熵是 :
D ( p ∣ ∣ q ) = ∑ x p ( x ) l o g p ( x ) q ( x ) = E p ( x ) l o g p ( x ) q ( x ) D(p||q)=\sum_{x}^{}p(x)log\frac{p(x)}{q(x)}={E}_{p(x)}log\frac{p(x)}{q(x)} D(p∣∣q)=x∑p(x)logq(x)p(x)=Ep(x)logq(x)p(x)

相对熵可以度量两个随机变量的“距离”。
一般的， D ( p ∣ ∣ q ) ≠ D ( q ∣ ∣ p ) D(p||q)\neq D(q||p) D(p∣∣q)=D(q∣∣p)。
D ( p ∣ ∣ q ) ≥ 0 ， D ( q ∣ ∣ p ) ≥ 0 D(p||q)\geq 0，D(q||p)\geq 0 D(p∣∣q)≥0，D(q∣∣p)≥0。

互信息

两个随机变量 X ， Y X，Y X，Y 的***互信息***，定义为 X ， Y X，Y X，Y 的***联合分布和独立分布乘积的相对熵***。
I ( X , Y ) = D ( P ( X , Y ) ∣ ∣ P ( x ) P ( Y ) I(X,Y)=D(P(X,Y)||P(x)P(Y) I(X,Y)=D(P(X,Y)∣∣P(x)P(Y)
I ( X , Y ) = ∑ x , y P ( x , y ) l o g P ( x , y ) p ( x ) p ( y ) I(X,Y)=\sum_{x,y}^{}P(x,y)log\frac{P(x,y)}{p(x)p(y)} I(X,Y)=x,y∑P(x,y)logp(x)p(y)P(x,y)

显然当 X , Y X,Y X,Y 互相独立时， P ( X , Y ) = P ( X ) P ( Y ) P(X,Y)=P(X)P(Y) P(X,Y)=P(X)P(Y) 这个时候， X , Y X,Y X,Y距离最短，互信息为零。

信息增益

信息增益表示得知特征 A A A 的信息而使得类 X X X 的信息的不确定性减少的程度。

定义：特征 A A A 对训练数据集 D D D 的信息增益 g ( D , A ) g(D,A) g(D,A)，定义为集合 D D D 的经验熵 H ( D ) H(D) H(D) 与特征 A A A 给定条件下 D D D 的经验条件熵 H ( D ∣ A ) H(D|A) H(D∣A) 之差，即：
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A)=H(D)-H(D|A) g(D,A)=H(D)−H(D∣A)

对于两个随机变量 X , Y X,Y X,Y，关于熵和互信息的一些总结公式：

H ( Y ∣ X ) = H ( X , Y ) − H ( X ) H(Y|X)=H(X,Y)-H(X) H(Y∣X)=H(X,Y)−H(X)
H ( Y ∣ X ) = H ( Y ) − I ( X , Y ) H(Y|X)=H(Y)-I(X,Y) H(Y∣X)=H(Y)−I(X,Y)
H ( Y ∣ X ) < H ( Y ) H(Y|X)<H(Y) H(Y∣X)<H(Y)
H ( X ∣ Y ) < H ( X ) H(X|Y)<H(X) H(X∣Y)<H(X)
I ( X , Y ) = H ( X ) + H ( Y ) − H ( X , Y ) I(X,Y)=H(X)+H(Y)-H(X,Y) I(X,Y)=H(X)+H(Y)−H(X,Y)

显然，这即为训练数据集 D D D 和特征 A A A 的互信息。

贝叶斯公式和最大后验估计

贝叶斯估计是一种生成式模型。所谓生成式和判别式模型的区别在于：

通过 P ( y ∣ x ) P(y|x) P(y∣x) 直接得出的模型称为判别式模型。
P ( y ∣ x ) P(y|x) P(y∣x) 是由 P ( x ∣ y ) P(x|y) P(x∣y) 得出的模型叫做生成式模型，也就是在类别已知的情况下，样本是怎么生成出来的。

P ( A ∣ D ) = P ( D ∣ A ) p ( D ) P(A|D)=\frac{P(D|A)}{p(D)} P(A∣D)=p(D)P(D∣A)

给定某些样本 D D D ，在这些样本中计算某结论 A 1 、 A 2 … … A n A1、 A2……An A1、A2……An 出现的概率，即 P ( A i ∣ D ) P(Ai|D) P(Ai∣D)。

第一个等式：贝叶斯公式；
第二个等式：样本给定，则对于任何 A i , P ( D ) Ai,P(D) Ai,P(D) 是常数，即分母仅为归一化因子
第三个箭头：若这些结论 A 1 、 A 2 … … A n A1、A2……An A1、A2……An 的先验概率相等 (或近似)，***即 P ( A 1 ) = P ( A 2 ) = . . . P ( A n ) P({A}_{1})=P({A}_{2})=...P({A}_{n}) P(A1)=P(A2)=...P(An)***，则得到最后一个等式：即第二行的公式，这时候其实是转成了求最大似然估计。

朴素贝叶斯

朴素贝叶斯的假设

一个特征出现的概率，与其他特征(条件)独立 (特征独立性)

其实是：对于给定分类的条件下，特征独立

每个特征***同等重要***(特征均衡性)

朴素贝叶斯的推导

朴素贝叶斯(Naive Bayes，NB)是基于“特征之间是独立的”这一朴素假设，应用贝叶斯定理的***监督学习*** 算法。

对于给定的特征向量 X 1 , X 2 , . . . , X n {X}_{1},{X}_{2},...,{X}_{n} X1,X2,...,Xn

类别 y y y 的概率可以根据贝叶斯公式得到：

使用朴素的***独立性*** 假设：
P ( x i ∣ y , x 1 , . . . , x i − 1 , x i + 1 , . . . , x n ) = P ( x i ∣ y ) P({x}_{i}|y,{x}_{1},...,{x}_{i-1},{x}_{i+1},...,{x}_{n})=P({x}_{i}|y) P(xi∣y,x1,...,xi−1,xi+1,...,xn)=P(xi∣y)

类别 y y y 的概率可简化为：
P ( y ∣ x 1 , x 2 , . . , x n ) = P ( y ) P ( x 1 , x 2 , . . . , x n ∣ y ) p ( x 1 , x 2 , . . . , x n ) = P ( y ) ∏ i = 1 n P ( x i ∣ y ) p ( x 1 , x 2 , . . . , x n ) P(y|{x}_{1},{x}_{2},..,{x}_{n})=\frac{P(y)P({x}_{1},{x}_{2},...,{x}_{n}|y)}{p({x}_{1},{x}_{2},...,{x}_{n})}=\frac{P(y)\prod_{i=1}^{n}P({x}_{i}|y)}{p({x}_{1},{x}_{2},...,{x}_{n})} P(y∣x1,x2,..,xn)=p(x1,x2,...,xn)P(y)P(x1,x2,...,xn∣y)=p(x1,x2,...,xn)P(y)∏i=1nP(xi∣y)

在给定样本的前提下， p ( x 1 , x 2 , . . . , x n ) p({x}_{1},{x}_{2},...,{x}_{n}) p(x1,x2,...,xn) 是常数：
P ( y ∣ x 1 , x 2 , . . . , x n ) ∝ P ( y ) ∏ i = 1 n P ( x i ∣ y ) P(y|{x}_{1},{x}_{2},...,{x}_{n})\propto P(y)\prod_{i=1}^{n}P({x}_{i}|y) P(y∣x1,x2,...,xn)∝P(y)i=1∏nP(xi∣y)

从而：
y ^ = a r g m a x P ( y ) ∏ i = 1 n P ( x i ∣ y ) \hat{y}=arg\ maxP(y)\prod_{i=1}^{n}P({x}_{i}|y) y^=arg maxP(y)i=1∏nP(xi∣y)

以上就是朴素贝叶斯通用化的推导，所有的朴素贝叶斯都可以这样推导出来。

根据样本使用 M A P ( M a x i m u m A P o s t e r i o r i ) MAP(Maximum A Posteriori) MAP(MaximumAPosteriori) 估计 P ( y ) P(y) P(y)，建立合理的模型估计 P ( x i ∣ y ) P({x}_{i}|y) P(xi∣y)，从而得到样本的类别。 y ^ = a r g m a x P ( y ) ∏ i = 1 n P ( x i ∣ y ) \hat{y}=arg\ maxP(y)\prod_{i=1}^{n}P({x}_{i}|y) y^=arg maxP(y)i=1∏nP(xi∣y)

高斯朴素贝叶斯

假设特征服从高斯分布，即：

参数使用 M L E MLE MLE （最大似然估计）估计即可。

多项分布朴素贝叶斯

假设特征服从多项分布，从而，对于每个类别y，参数为 θ y = ( θ y 1 , θ y 2 , θ y 2 , . . . , θ y n ) {\theta }_{y}=({\theta }_{y1},{\theta }_{y2},{\theta }_{y2},...,{\theta }_{yn}) θy=(θy1,θy2,θy2,...,θyn)，其中 n n n 为特征的数目， P ( x i ∣ y ) P({x}_{i}|y) P(xi∣y) 的概率为 , θ y i ,{\theta }_{yi} ,θyi。

参数 θ y i {\theta }_{yi} θyi 使用 M L E MLE MLE 估计的结果为：

假定训练集为 T T T，有:

其中：

α = 1 \alpha =1 α=1 称为 L a p l a c e Laplace Laplace 平滑。
α < 1 \alpha <1 α<1 称为 L i d s t o n e Lidstone Lidstone 平滑。
平滑操作除了避免出现零，还有增加模型的泛化能力的作用。

以文本分类为例

问题描述

样本： 1000 1000 1000 封邮件，每个邮件被标记为垃圾邮件或者非垃圾邮件。
分类目标：给定第 1001 1001 1001 封邮件，确定它是垃圾邮件还是非垃圾邮件。
方法：朴素贝叶斯

问题分析

类别 c c c ：垃圾邮件 c 1 c1 c1，非垃圾邮件 c 2 c2 c2。
词汇表，两种建立方法：

使用现成的单词词典；
将所有邮件中出现的单词都统计出来，得到词典。

记单词数目为 N N N 。

将每个邮件 m m m 映射成维度为 N N N 的向量 x x x。

若单词 w i wi wi 在邮件 m m m 中出现过，则 x i = 1 xi=1 xi=1，否则， x i = 0 xi=0 xi=0。即邮件的向量化： m = ( x 1 , x 2 … … x N ) m=(x1,x2……xN) m=(x1,x2……xN)

贝叶斯公式： P ( c ∣ x ) = P ( x ∣ c ) ∗ P ( c ) / P ( x ) P(c|x)=P(x|c)*P(c) / P(x) P(c∣x)=P(x∣c)∗P(c)/P(x) ，注意这里 x x x 是向量。

特征独立假设： P ( x ) = P ( x 1 , x 2 … x N ) = P ( x 1 ) ∗ P ( x 2 ) … P ( x N ) P(x)=P(x1,x2…xN)=P(x1)*P(x2)…P(xN) P(x)=P(x1,x2…xN)=P(x1)∗P(x2)…P(xN)

带入公式： P ( c ∣ x ) = P ( x ∣ c ) ∗ P ( c ) / P ( x ) P(c|x)=P(x|c)*P(c) / P(x) P(c∣x)=P(x∣c)∗P(c)/P(x)
实际情况下，不需要考虑 P ( x ) P(x) P(x)，故只剩下***特征条件独立假设***。

等式右侧各项的含义：

P ( x i ∣ c j ) P(xi|cj) P(xi∣cj)：在 c j cj cj (此题目， c j cj cj 要么为垃圾邮件1，要么为非垃圾邮件2)的前提下，第 i i i 个单词 x i xi xi出现的概率。
P ( x i ) P(xi) P(xi) ：在所有样本中，单词 x i xi xi 出现的概率。
P ( c j ) P(cj) P(cj) ：在所有样本中，邮件类别 c j cj cj 出现的概率。

由上面例子可以看出，朴素贝叶斯基于以下两条假设：

一个特征出现的概率，与其他特征(条件)独立(特征独立性)，即是：对于给定分类的条件下，特征独立。
每个特征同等重要(特征均衡性) 。

以上两条假设不一定正确，但是基于这两条假设的朴素贝叶斯在一些应用中效果却是不错的。

贝叶斯网络

把某个研究系统中涉及的随机变量，根据是否***条件独立*** 绘制在一个***有向图*** 中，就形成了贝叶斯网络。

贝叶斯网络( B a y e s i a n N e t w o r k Bayesian Network BayesianNetwork)，又称有向无环图模型 ( d i r e c t e d a c y c l i c g r a p h i c a l m o d e l , D A G ) (directed\ acyclic\ graphical\ model ,DAG) (directed acyclic graphical model,DAG)，是一种概率图模型，根据概率图的拓扑结构，考察一组随机变量 X 1 , X 2... X n {X1,X2...Xn} X1,X2...Xn 及其 n n n 组条件概率分布
( C o n d i t i o n a l P r o b a b i l i t y D i s t r i b u t i o n s , C P D ) (Conditional\ Probability\ Distributions, CPD) (Conditional Probability Distributions,CPD) 的性质。

一般而言，贝叶斯网络的有向无环图中的节点表示随机变量，它们可以是可观察到的变量，或隐变量、未知参数等。连接两个节点的箭头代表此两个随机变量是具有***因果关系(或非条件独立***)。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因 ( p a r e n t s ) (parents) (parents)”，另一个是“果 ( c h i l d r e n ) (children) (children)”，两节点就会产生一个条件概率值。

每个结点在给定其直接前驱时，条件独立 于其非后继。

一个简单的贝叶斯网络

P ( a , b , c ) = P ( c ∣ a , b ) P ( b ∣ a ) P ( a ) P(a,b,c)=P(c|a,b)P(b|a)P(a) P(a,b,c)=P(c∣a,b)P(b∣a)P(a)，其对应的无向图如下：

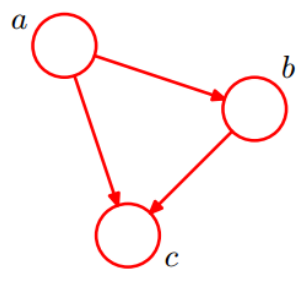
![这里写图片描述](https://img-blog.csdnimg.cn/img_convert/5abf3a46467d427ac4a5628231052592.png)

P ( x 1 , x 2 , x 3 , x 4 ∣ y ) = P ( x 1 ∣ y ) ∗ P ( x 2 ∣ y ) ∗ P ( x 3 ∣ y ) ∗ P ( x 4 ∣ y ) P({x}_{1},{x}_{2},{x}_{3},{x}_{4}|y)=P({x}_{1}|y)*P({x}_{2}|y)*P({x}_{3}|y)*P({x}_{4}|y) P(x1,x2,x3,x4∣y)=P(x1∣y)∗P(x2∣y)∗P(x3∣y)∗P(x4∣y)，其对应的无向图如下：

朴素贝叶斯就是把特征 ( x 1 , x 2 , x 3 , x 4 ) (x1,x2,x3,x4) (x1,x2,x3,x4)之间的有向边都删掉了。

全连接贝叶斯网络

每一对结点之间都有边连接：

一个“正常”的贝叶斯网络：

有些边缺失
直观上：
x 1 x1 x1 和 x 2 x2 x2 独立
x 6 x6 x6 和 x 7 x7 x7 在 x 4 x4 x4 给定的条件下独立
x 1 , x 2 , … x 7 x1,x2,…x7 x1,x2,…x7 的联合分布：

对一个实际贝叶斯网络的分析：

贝叶斯网络的形式化定义

B N ( G , Θ ) BN(G, Θ) BN(G,Θ)

G:有向无环图
G的结点：随机变量
G的边：结点间的***有向依赖***
Θ：所有条件概率分布的参数集合
结点 X X X 的条件概率： P ( X ∣ p a r e n t ( X ) ) P(X|parent(X)) P(X∣parent(X))

通过贝叶斯网络判定条件独立—1

根据图模型，得： P ( a , b , c ) = P ( c ) ∗ P ( a ∣ c ) ∗ P ( b ∣ c ) P(a,b,c)=P(c)*P(a|c)*P(b|c) P(a,b,c)=P(c)∗P(a∣c)∗P(b∣c)
从而： P ( a , b , c ) / P ( c ) = P ( a ∣ c ) ∗ P ( b ∣ c ) P(a,b,c)/P(c)= P(a|c)*P(b|c) P(a,b,c)/P(c)=P(a∣c)∗P(b∣c)
因为 P ( a , b ∣ c ) = P ( a , b , c ) / P ( c ) P(a,b|c)=P(a,b,c)/P(c) P(a,b∣c)=P(a,b,c)/P(c)
得： P ( a , b ∣ c ) = P ( a ∣ c ) ∗ P ( b ∣ c ) P(a,b|c)=P(a|c)*P(b|c) P(a,b∣c)=P(a∣c)∗P(b∣c)

即：在 c c c 给定的条件下， a ， b a，b a，b 被阻断 ( b l o c k e d ) (blocked) (blocked) 是独立的。

通过贝叶斯网络判定条件独立—2

P ( a , b , c ) = P ( a ) ∗ P ( c ∣ a ) ∗ P ( b ∣ c ) P(a,b,c)=P(a)*P(c|a)*P(b|c) P(a,b,c)=P(a)∗P(c∣a)∗P(b∣c)

即：在 c c c 给定的条件下， a ， b a，b a，b 被阻断(blocked)，是独立的。

通过贝叶斯网络判定条件独立—3

在 c c c 未知的条件下， a ， b a，b a，b 被阻断(blocked)，是独立的： head-to-head

以上三种情况的举例说明：